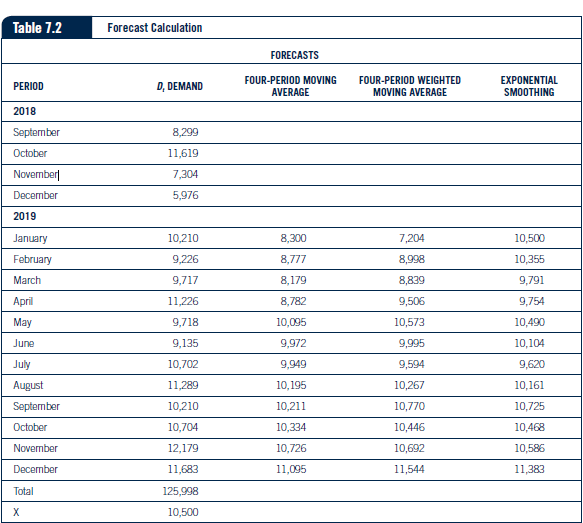
Question: A, = 0.60D, + 0.20D._ ( + 0.15D,, + 0.05D 1-3 7.7 Column 4 in Table 7.2 shows the results of this formula. The weighted
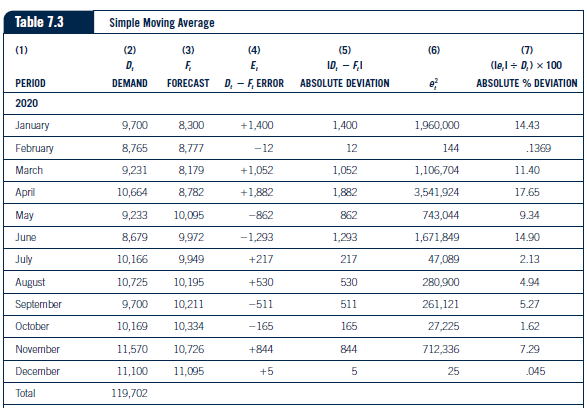
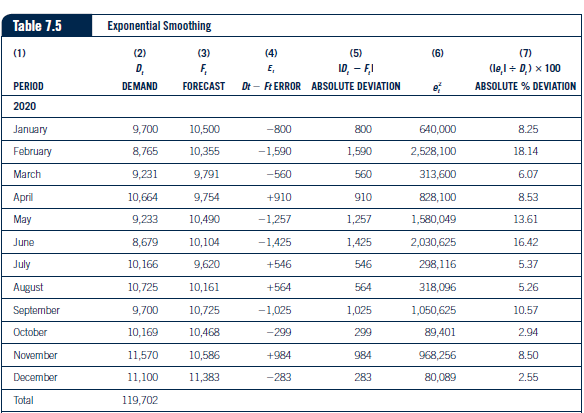
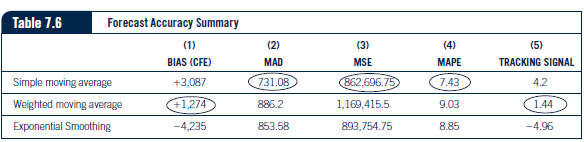
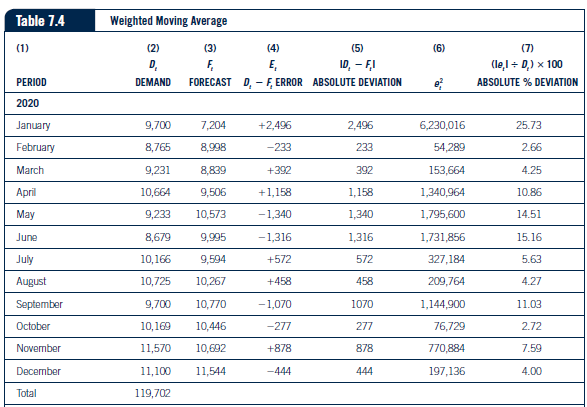
A, = 0.60D, + 0.20D._ ( + 0.15D,, + 0.05D 1-3 7.7 Column 4 in Table 7.2 shows the results of this formula. The weighted moving average for January would be calculated as follows: (0.60 X 5,976) + (0.20 X 7,304) + (0.15 X 11,619) + (0.05 X 8,299) = 7.204Table 7.2 Forecast Calculation FORECASTS PERIOD D. DEMAND FOUR-PERIOD MOVING FOUR-PERIOD WEIGHTED EXPONENTIAL AVERAGE MOVING AVERAGE SMOOTHING 2018 September 8,299 October 11,619 November DOEL December 5,976 2019 January 10,210 8,300 7,204 10,500 February 9.226 8,777 8,998 10,355 March 9,717 8,179 8,839 9,791 April 11,226 B,782 9,506 9,754 May 9,718 10,095 10,573 10,490 June 9,135 9.972 9,995 10,104 July 10,702 9.949 9,594 9.620 August 11,289 10,195 10,267 10,161 September 10.210 10,211 10,770 10,725 October 10,704 10,334 10,446 10,468 November 12,179 10,726 10,692 10,586 December 11,683 11,095 11,544 11,383 Total 125,998 X 10,500This measure is also calculated in Tables 7.2 through 7.4. By taking the absolute value of each error, the negative and positive signs are removed and a good indication of average error per period is calculated. This measure is popular because it is easy to understand and provides a good indication of the accuracy of the forecast. Another measure of forecast error is mean absolute percent error (MAPE). MAPE can be calculated using Formula 7.4. MAPE = E (E, VD, )100 7.4 Finally, tracking signal can be used to measure forecast error. It is especially good at identifying if a bias exists in the forecast errors and can be calculated using Formula 7.5. Tracking signal = Cumulative forecast error (CFE )/Mean absolute deviation (MAD) 7.5Table 7.3 Simple Moving Average (1) (2) (3) (4) (5) (6) (7) D. F 10, - FI (lel = D.) x 100 PERIOD DEMAND FORECAST D. - F, ERROR ABSOLUTE DEVIATION ABSOLUTE % DEVIATION 2020 January 9,700 8,300 +1,400 1,400 1,960,000 14.43 February 8,765 8,777 -12 12 144 1360 March 9,231 8.179 +1,052 1,052 1,106,704 11.40 April 10,664 8,782 +1,882 1,882 3,541,924 17.65 May 9,233 10,095 -862 862 743.044 9.34 June 8,679 9,972 -1,293 1,293 1,671,849 14.90 July 10,166 9,949 +217 217 47,089 2.13 August 10,725 10,195 +530 530 280,900 4.94 September 9,700 10,211 -511 511 261,121 5.27 October 10,169 10,334 -165 165 27,225 1.62 November 11,570 10,726 +844 844 712,336 7.29 December 11,100 11,095 +5 5 25 045 Total 119,702F+1 = F+ + a(At - Ft) F+ +1 aA + + 1 - a Ft7-5 Forecast Errors As previously mentioned, almost all forecasts will be wrong. Some forecasts will be higher than demand, and some will be lower. Managing the forecasting process requires minimizing the errors between actual demand and forecasted demand. The key to success- ful forecasting is to choose the technique that provides the least amount of forecast error. To determine which forecasting technique is best for a set of data, the forecast error must be measured. Four types of forecast error measures can be used. The first is called the cumulative sum of forecast errors (CFE) and can be calculated using Formula 7.1. CFE = 7.1 CFE calculates the total forecast error for a set of data, taking into consideration both negative and positive errors. This is also referred to as bias and was used in Tables 7.2 through 7.4. This gives an overall measure of forecast error. However, taking into consider- ation both negative and positive errors, this method can produce an overall low error total although individual period forecasts can either be much higher or much lower than actual demand. The second measure of forecast error is mean squared error (MSE). This measure can be calculated using Formula 7.2. SE MSE = 7.2 This measure squares each period error so the negative and positive errors do not cancel each other out. MSE also provides a good indication of the average error per period over a set of demand data. Closely related to MSE is the third type of forecast error measure, mean absolute deviation (MAD). It can be calculated using Formula 7.3. MAD = EIEI 7.3Table 7.5 Exponential Smoothing (1) (2) (3) (4) (5) (6) (7) D. F. E ID, - FI (le,1 = D) x 100 PERIOD DEMAND FORECAST De - At ERROR ABSOLUTE DEVIATION ABSOLUTE % DEVIATION 2020 January 9,700 10,500 -800 800 640,000 8.25 February 8,765 10,355 -1,590 1,590 2,528,100 18.14 March 9,231 9,791 -560 560 313,600 6.07 April 10,664 9,754 +910 910 828,100 8.53 May 9,233 10,490 -1,257 1,257 1,580,049 13.61 June 8,679 10,104 -1,425 1,425 2,030,625 16.42 July 10,166 9,620 +546 546 298,116 5.37 August 10,725 10,161 +564 564 318,096 5.26 September 9,700 10,725 -1,025 1,025 1,050,625 10.57 October 10,169 10,468 -299 299 89,401 2.94 November 11,570 10,586 +984 984 968,256 8.50 December 11,100 11,383 -283 283 80,089 2.55 Total 119,702Table 7.6 Forecast Accuracy Summary (1) (2) (3) (4) (5) BIAS (CFE) MAD MSE MAPE TRACKING SIGNAL Simple moving average +3,087 731.08 (862,696.75) 7.43 4.2 Weighted moving average +1,274 886.2 1,169,415.5 9.03 1.44 Exponential Smoothing -4,235 853.58 893,754.75 8.85 -4.96Table 7.4 Weighted Moving Average (1) (2) (3) (4) (5) (6) (7) F E, ID, - FI (le, I + D,) x 100 PERIOD DEMAND FORECAST D, - F. ERROR ABSOLUTE DEVIATION ABSOLUTE % DEVIATION 2020 January 9,700 7,204 +2.496 2,496 6,230,016 25.73 February 8,765 8,998 -233 233 54,289 2.66 March 9,231 8.839 +392 392 153,664 4.25 April 10,664 9,506 +1,158 1,158 1,340,964 10.86 May 9,233 10,573 -1,340 1,340 1,795,600 14.51 June 8,679 9.995 -1,316 1,316 1,731,856 15.16 July 10,166 9,594 +572 572 327,184 5.63 August 10,725 10 267 +458 458 209,764 4.27 September 9,700 10,770 -1,070 1070 1,144,900 11.03 October 10,169 10,446 -277 277 76,729 2.72 November 11,570 10,692 +878 878 770,884 7.59 December 11,100 11,544 -444 444 197,136 4.00 Total 119,702