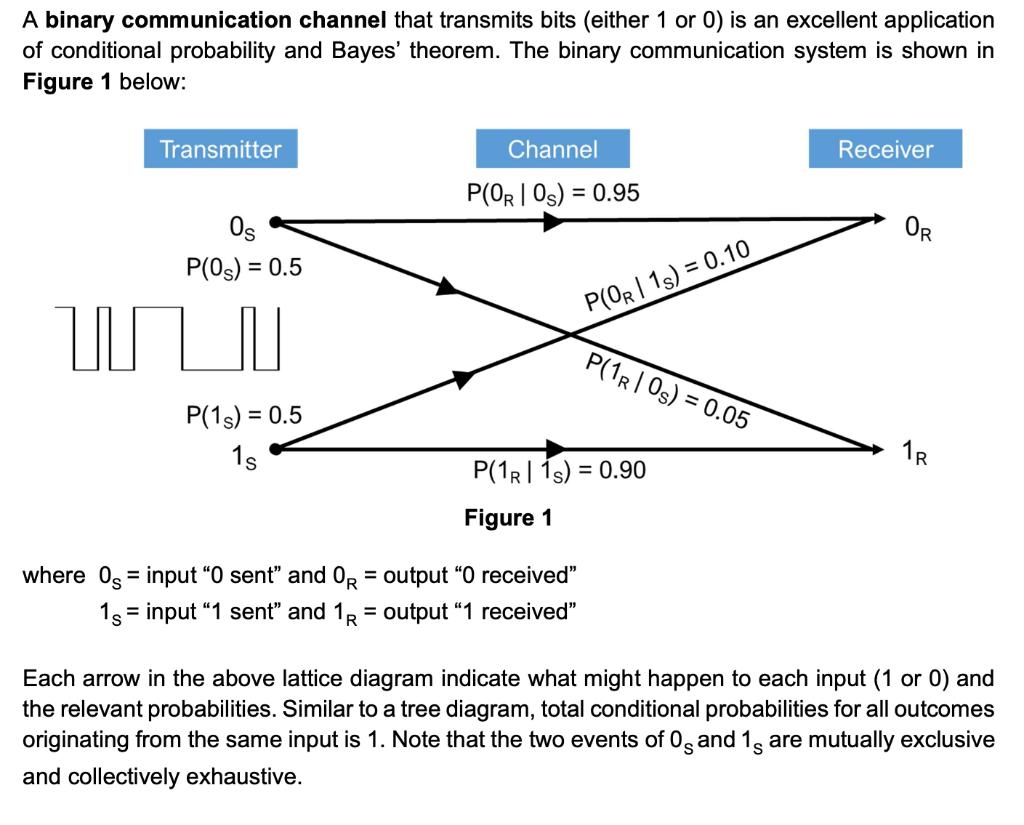
A binary communication channel that transmits bits (either 1 or 0) is an excellent application of conditional probability and Bayes' theorem. The binary communication system is shown in Figure 1 below: Transmitter Channel Receiver P(OR | Os) = 0.95 Os OR P(0s) = 0.5 P(OR | 1s) = 0.10 P(1R| Os) = 0.05 P(1s) = 0.5 1s 1R P(1R| s) = 0.90 Figure 1 where 0s = input "0 sent" and 0R = output "O received" %3D %3D 1s = input "1 sent" and 1R = output "1 received" Each arrow in the above lattice diagram indicate what might happen to each input (1 or 0) and the relevant probabilities. Similar to a tree diagram, total conditional probabilities for all outcomes originating from the same input is 1. Note that the two events of 0 and 1, are mutually exclusive and collectively exhaustive. B) Theoretical Calculation To understand the behavior of the binary channel, answer the following questions: 1) Identify the equation and value of the following probabilities from Figure 1: a) P (a 0 is transmitted, it is correctly received) = b) P (a 0 is transmitted, it is incorrectly received) = c) Prior probability of 0 transmitted = d) Prior probability of 1 sent = e) P (a 1 is transmitted, but 0 is received) = 2) An error occurs when each input transmitted is incorrectly received at the receiver, eg. a 1 is transmitted but a 0 signal is received. The probability of error, P(error) is an overall measure of performance, frequently used in communication systems. For an optimal system, P(error) should be minimized. Using total probability theorem, calculate P(error) for the channel in Figure 1. P(error) = P (0RI 1s) P (1s) + P (1R | Os) P (0s) P(error) = 3) If the binary channel is designed correctly, P (1s | 1R) > P (0s | 1R)*. The same relationship applies for OR. * read as probability that a "1" was sent given that a "1" is received is greater than the probability that a "0" was sent given that a "1" is received. Prove the above statement is true for the binary channel in Figure 1. Do you agree that this is a good condition for the channel? Why?