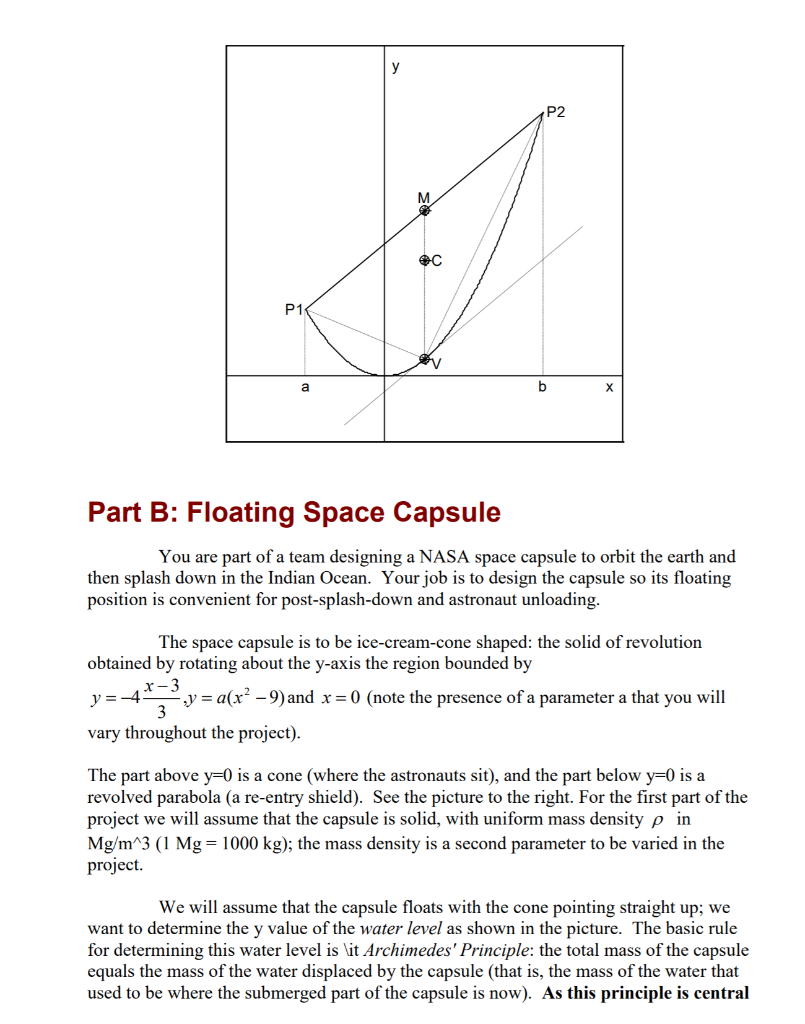
Question: ( a ) Determine the water level as a function of the mass density and a ( p 1 for this part ) as follows.
a Determine the water level as a function of the mass density and a p for this part as follows. Determine via a definite integral the volume of the capsule from its bottom
ya to an arbitrary height y for a y ; call this Vy
Note that you need a different formula for a y and y If the capsule is submerged up to y then Vy also gives the mass of water displaced since the density of
water is
Thus, the water level is the value of y call it y for which Vy equals the total mass of
the capsule. Split into cases depending on whether V is greater than or less than the
total mass of the capsule.
b For p what must a be in order for the water level to be y What about for
p Can you explain the change between these two cases from the physical problem? For fixed a what happens to the water level y as p approaches Does that
make physical sense?
The center plane' of the capsule is the value of y yc so that half of the capsule's mass is above y yc and half below it Given your function Vy you can determine c y from
this definition, or it is probably easier to use the formula
Total Mass of Capsule
where dVy is the volume of the cross section at position y with width dy
The centerofbuoyancy plane' of the submerged capsule is the value of y yc so that half of the mass of the displaced water is above y yb and half below it The
corresponding integral now in terms of the water level y is
Total Mass of Water Displaced by the Capsule
where dVy is again the volume of the crosssection at position y
Buoyancy theory suggests that the submerged capsule will be most stable if the center
plane is below the centerofbuoyancy plane.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


