Question: A discount function is defined as follows:-(t)=1/(1 + .016), where t > 0. A five-year annuity has payments of 1 times, t 1.2.3. 4. and

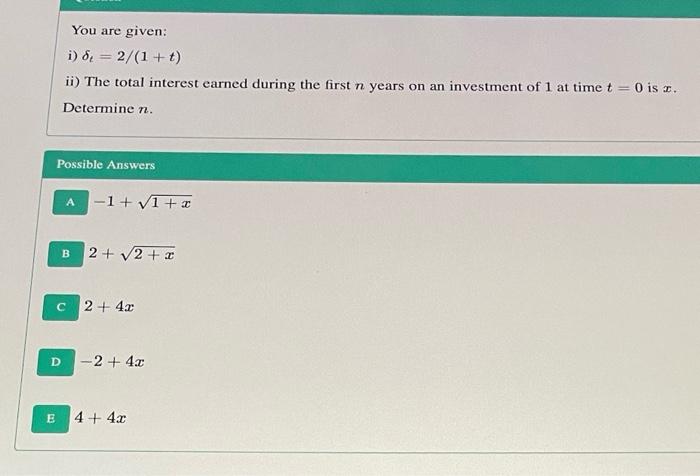
A discount function is defined as follows:-(t)=1/(1 + .016), where t > 0. A five-year annuity has payments of 1 times, t 1.2.3. 4. and 5 To calculate the present value of the annuity, a student first accumulates the payments according to the following accumulation function, where is the length of the accumulation period: a() - 1+.01. The student then multiplies the result by a (5) By how much does the student's calculated value exceed the correct value of the annuity at time t = 0? (Answer to nearest .0001) Possible Answers - 0494 -.0018 0 _0018 .0494 You are given: i) 8 = 2/(1+t) ii) The total interest earned during the first n years on an investment of 1 at time t = 0 is B. Determine n. Possible Answers -1++ B B 2+2+ 2 + 4.2 D-2 + 4.C E 4+ 4.2

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

Operations Effectiveness. Does it appear that the Mayo Clinic management team is operating effectively as a nonprofit organization? Are they controlling operations? Why or why not? What evidence can...

Burses Luis Integration Documentation ENGR 1221 - Programming Matlab (6595) > Exercise 6 > Problem 2 O solutions submitted (max Unlimited) Present Value of an Annuity Retirees often purchase an...

2. Future value Aa Aa The principal of the time value of money is probably the single most important concept in financial management. One of the most frequently encountered applications involves the...

Please just help me correct the ones that I got wrong. Please, and thank you. The corrections are in the file seboprincess00322885. I made some corrections already so if you come across them, just...

Problem 15.32 For time t > 0, the discount function is defined by [a(t)]-i = . 1+0.01t Consider a five-year annuity with payments of 1 at times t = 1, 2, 3, 4, 5, Consider the following: A calculates...

8.1. Dulles Electric Company buys 1 million tons of coal annually to burn at its power plant. The company wants to invest in a unit train that will haul coal from the mine to the power house, where...

6.1. Carbondale Company has the following credit policy 2/10, net 30. Carbondale also charges 1% per month interest on all accounts after 30 days. The following table shows the collection schedule of...

Hi Erylee88, I would like to utilize your service again. Same format different questions. Please find attached document for your review. Let me know. Thank you, Sam...

SEE "DOCUMENT 1" FOR CRITERIA 2 "DOCUMENT 2" FOR CRITERIA 4 You are to write a 3 to 4 page paper following APA rules for the title page, citations and appropriate references within the body of the...

Nowadays, we can choose either a laptop computer or a tablet to be a portable electronic device. Recently, the consumers of those electronics devices find that the price of tablets increases sharply....

Decker & Co. makes electronic components. Chris Decker, the president, recently instructed Vice President Jim Bruegger to develop a total quality control program. If we dont at least match the...

Equations that contain one or more algebraic fractions are known as fractional equations. To solve a fractional equation that can be reduced to a quadratic equation: Multiply both sides of the...

Which of the following statement ( s ) is / are true for gradient descent and stochastic gradient decent? In both batch gradient descent and stochastic gradient descent, the unknown variables are...