Question: (a) Let T : R2 -> R be the transformation that rotates a vector 3 counterclockwise. The transformation matrix for this linear transformation is: 1/2

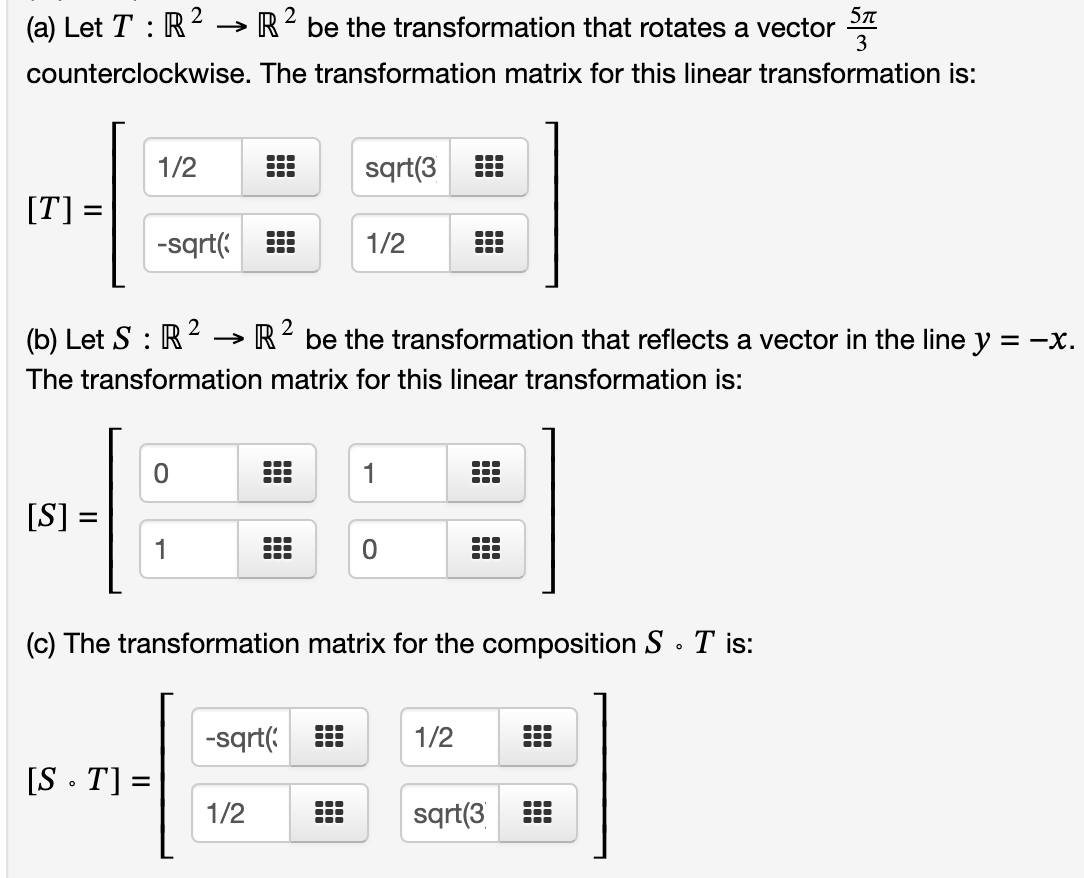
(a) Let T : R2 -> R be the transformation that rotates a vector 3 counterclockwise. The transformation matrix for this linear transformation

is: 1/2 sqrt(3 [T] = -sqrt(: 1/2 (b) Let S : R

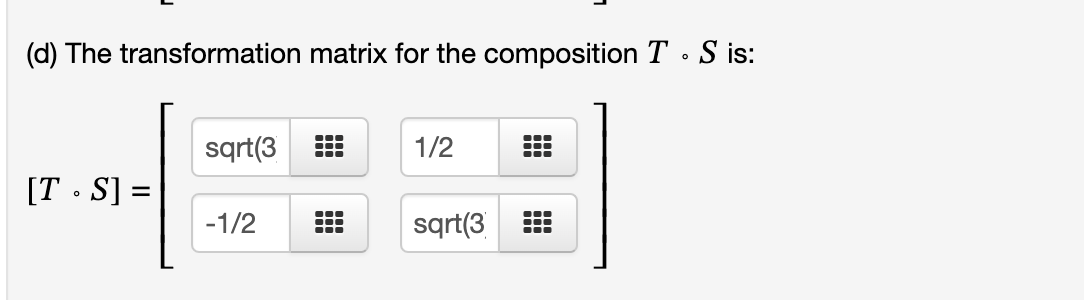
-> R be the transformation that reflects a vector in the line

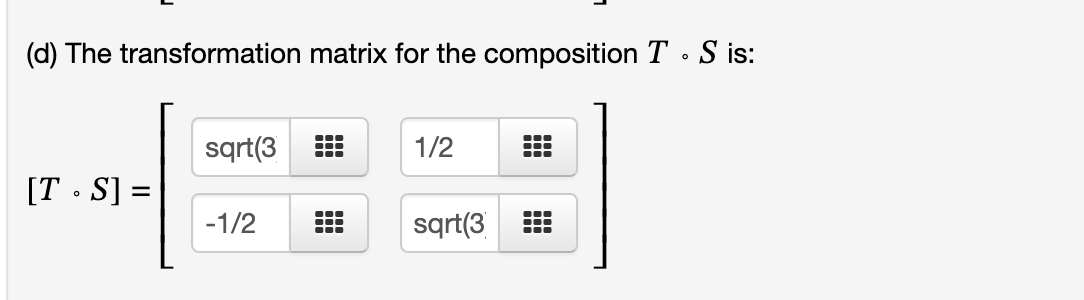
(a) Let T : R2 -> R be the transformation that rotates a vector 3 counterclockwise. The transformation matrix for this linear transformation is: 1/2 sqrt(3 [T] = -sqrt(: 1/2 (b) Let S : R -> R be the transformation that reflects a vector in the line y = -X. The transformation matrix for this linear transformation is: 0 [S] = 1 0 (c) The transformation matrix for the composition S . T is: -sqrt( 1/2 [S . T] = 1/2 sqrt(3(d) The transformation matrix for the composition T . S is: sqrt(3 1/2 [T . S] = -1/2 sqrt(3

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

0.57 points PA7-1 Analyzing the Effects of Four Alternative Inventory Methods in a Periodic Inventory System [LO 7-3] Gladstone Company tracks the number of units purchased and sold throughout each...

Hello dear tutors, I have a question that is regarding to Linear Algebra. It's a question from the textbook. I have already attached the screenshot as below. My question is: Why do SIN and COS flip...

8.1 WRITE on paper for upvote. Section: 25, 32, 33 please 8.1 General Linear Transformations 20. Consider the basis S = {V1, V2} for R', where v, = (-2, 1) and 9. T : Rx - R., where V2 = (1, 3), and...

To see that composition of two rotations about different coordination axes is equivalent to a single rotation about a fixed direction. M=[1 2 3; 4 5 6] Creates a certain 2 times 3 matrix and calls it...

In Exercise, show that the given transformation from R2 to R2 is linear by showing that it is a matrix transformation a. F reflects a vector in the y-axis. b. R rotates a vector 45 counterclockwise...

1. Indicate if the following functions ?: ?^2? ?^2 are linear transformations, justifying your answer. 1.1. ?(?, ?) = (1 + ?, ?). 1.2. ?(?, ?) = (?, ?) 1.3 ?(?, ?) = (?^2, ?) 1.4 ?(?, ?) = (????, ?)...

Please help me find the answers to the practice question and please provide work and number of question. -2 O 1: Consider matrix A = ONE 1 5 -3 . Find the following subspaces and a 1 3 basis for each...

(1) (3 points) Set u = 0 8 and set v = AOO (a) Compute the linear combination -2u + 5v. (b) Compute the dot product u . v. In problems (2) (3) below we use the standard definition of a "linear trans-...

please help to answer these 8 questions, thank you~ Question 1. In each of the following, determine if the given set is a subspace of R2 or not. For each case in which the set is a subspace, verify...

Linear Algebra Final answer only - No Explanation Section 4.2 Matrix of Transformations: Problem 7 :1 point: Find the malrix A of the linear transformation T from lit\" to R2 that rotates any...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

The August bank reconciliation for C& C Limited: Balance per bank..................... $ 151,570 Plus: outstanding deposits 17,900 Less: Outstanding cheques ($ 11,245, $ 650, $ 1,570, $ 890, $ 120).....

Higgins Corporation issues $1 million of 20-year, $1,000 face value, 10% semiannual coupon bonds at par on January 2, 2013. Each $1,000 bond is convertible into 40 shares of $1 par value common stock...

Find the angle between the vectors. u = - i + 2 j , v = - 4 i - 5 j + 3 k

What is entrepreneurship

Calculate / report the mean and standard deviation of NPV what is he probability that the project will have a positive NPV? What is the probability that NPV will exceed $10,000? What is the...

What key insights does the GEMS study provide us about entrepreneurship?

You have 500 data points, which are normally distributed with a mean of 400 and a standard deviation of 50. All scores are integers. Then one new data point is added, which is far above the top end...

It is evident that some call handlers are very unhappy and feel that their job is adversely affecting their mental health. The CCM is concerned and wants to take action to improve the situation. (a)...

Create a 200 word summary on the Juvenile Justice System than and today. Describe The Juvenile system and provide a generalizable definition. Highlight the issues in the Juvenile system and why this...

It has been said that prior department costs behave similarly to direct mate- rials costs. Under what conditions are the costs similar? What differences arise that require the costs to be treated...

Farleigh O. Tuvit is a new member of the controller's staff in the same company as you. Farleigh has just completed a report that urges the company to adopt the LIFO method for inventory accounting....

Describe methods for handling lost units in a process that expects certain losses due to shrinkage, evaporation, or other inherent characteristics of the process.