a. To determine the axial force in a statically indeterminate, axially loaded system and to learn about displacement compatibility. Statically indeterminate systems can be solved by combining the principles of statics (equilibrium equations) with a compatibility condition. This condition describes how displacements within the system are related based on the system's geometric constraints. (Figure 1). i. An infinitely rigid, weightless beam is supported by three circular posts, as shown. The outer posts are made of A-36 steel, and the central post is made of 2014-T6 aluminum. Before loading, all posts have a length of 250 mm. The system is subjected to a distributed load of 200 kN/mkN/m. Assume that the posts are rigidly connected to the beam and that the posts are subjected to the uniform, the distributed load applied to the beam. Find a compatibility condition that relates the displacement of the tops of the steel and aluminum posts due to the unknown axial forces in the posts. Let ?a be the displacement of the top of the aluminum post due to the axial force and ?s be the displacement of the top of the steel posts due to the axial force.

ii. Construct the equilibrium equation (in terms of force) that relates the axial load in the steel and aluminum posts to the distributed load applied to the beam. Let Fa and Fs equal the magnitudes of the force in each of the aluminum and steel posts, respectively.

iii. Determine the magnitude of the axial force in each of the steel and aluminum posts when subjected to the uniform distributed load. Treat compressive forces as negative and tensile forces as positive.

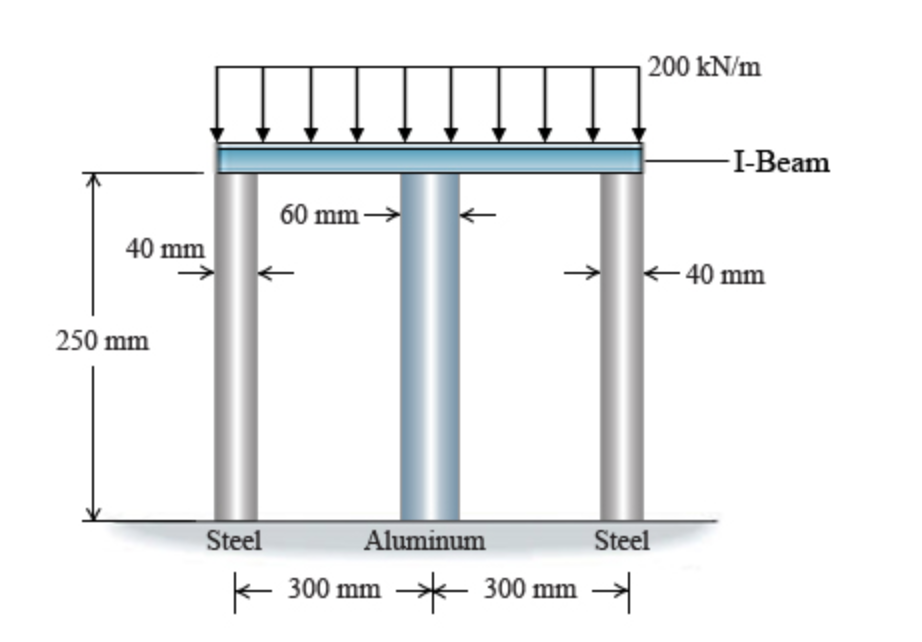
40 mm 60 mm 250 mm Steel Aluminum Steel 300 mm 300 mm 200 kN/m -I-Beam