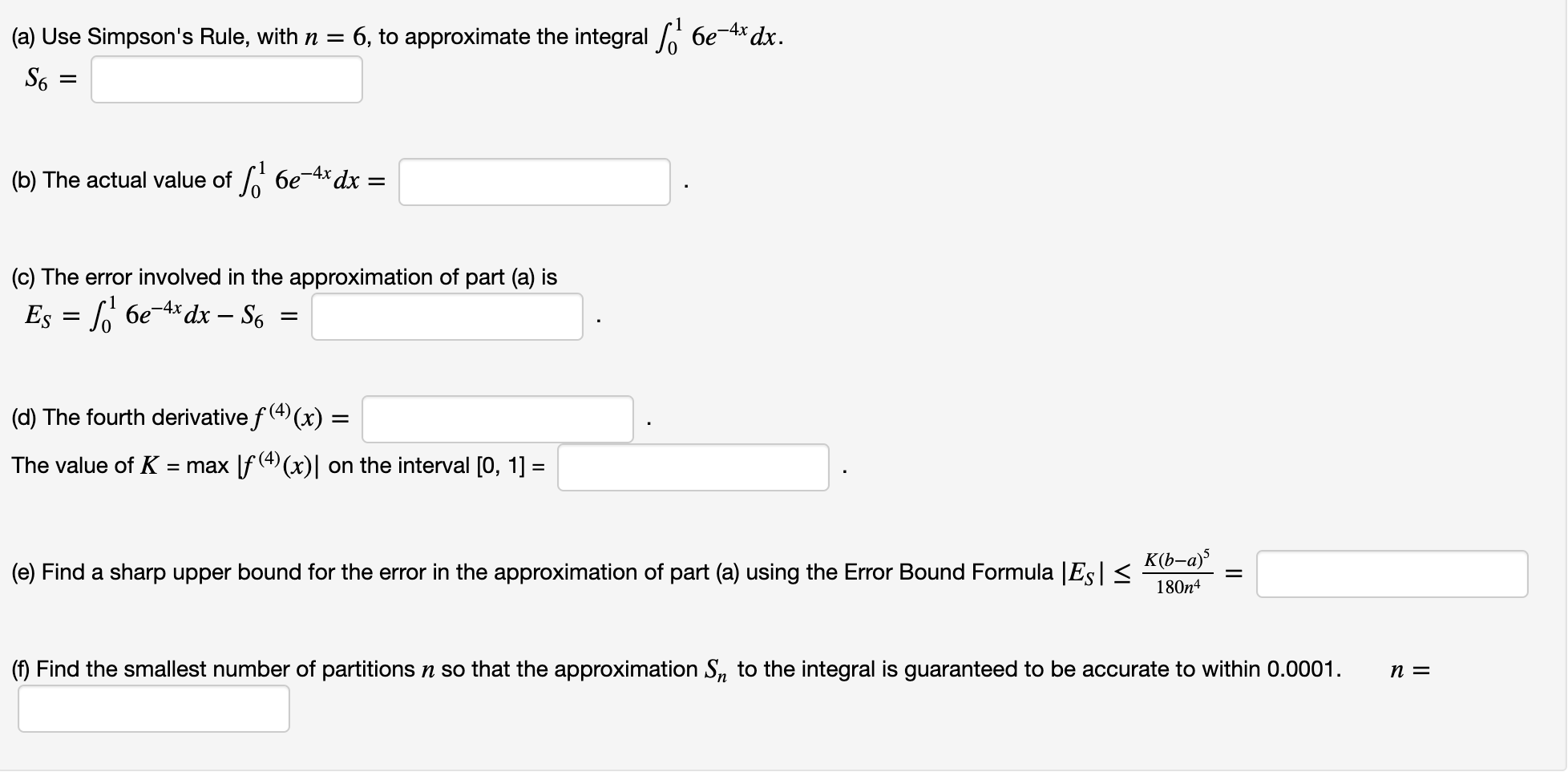
(a) Use Simpson's Rule, with n = 6, to approximate the integral 6e-4x dx. S6 = (b) The actual value of f 6e-4x dx = (c) The error involved in the approximation of part (a) is Es = 6e-4x dx - S6 = (d) The fourth derivative (4) (x) = The value of K = max [f(4)(x)| on the interval [0, 1] = (e) Find a sharp upper bound for the error in the approximation of part (a) using the Error Bound Formula |Es| K(b-a)5 180n4 = (f) Find the smallest number of partitions so that the approximation S, to the integral is guaranteed to be accurate to within 0.0001. n =