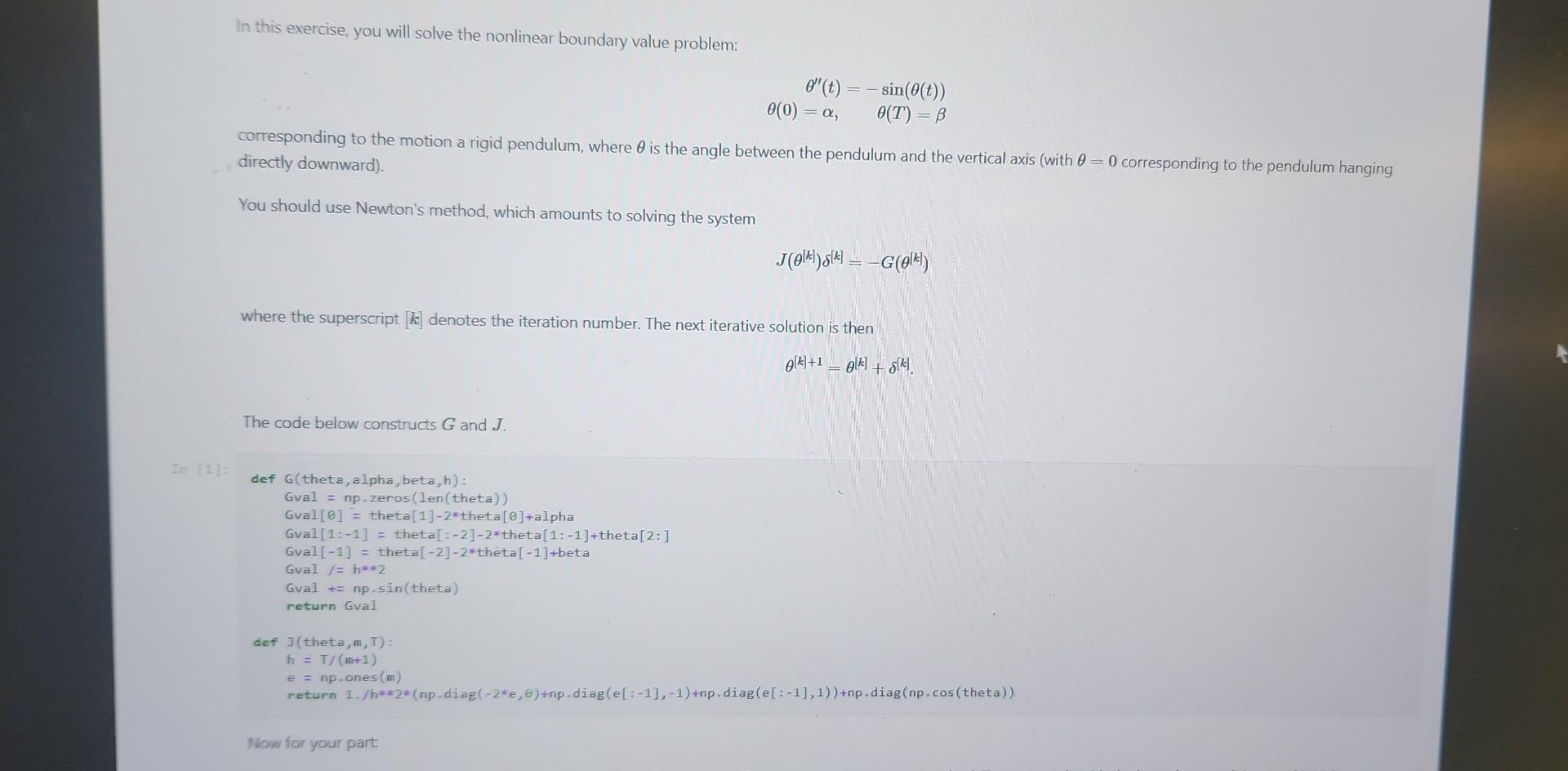
(a) Write a program that solves the problem above (for given values of T,, ) by using Newton's method. Test your code with the boundary conditions and initial guesses given in the textbook. (b) Try taking T larger (perhaps 6,8, or larger) and see what kinds of solutions you can find, by trying different initial guesses. You will probably observe that Newton's method is very sensitive to the initial guess and often diverges (note that if it's going to converge, it usually won't take more than 10 iterations to do so). Make sure your initial guess satisfies the boundary conditions, and try adjusting it until you find some solutions. Can you find two initial guesses that are very close but converge to very different final solutions? You may also find solutions that have "boundary layers" (see section 2.17 of the text, if you're interested). Explain what kind of physical motion each solution corresponds to. In this exercise, you will solve the nonlinear boundary value problem: (t)=sin((t))(0)=,(T)= corresponding to the motion a rigid pendulum, where is the angle between the pendulum and the vertical axis (with =0 corresponding to the pendulum hanging directly downward). You should use Newton's method, which amounts to solving the system J([k])[k]=G([k]) where the superscript [k] denotes the iteration number. The next iterative solution is then [k]+1=[k]+[k] The code below constructs G and J. Now for your part