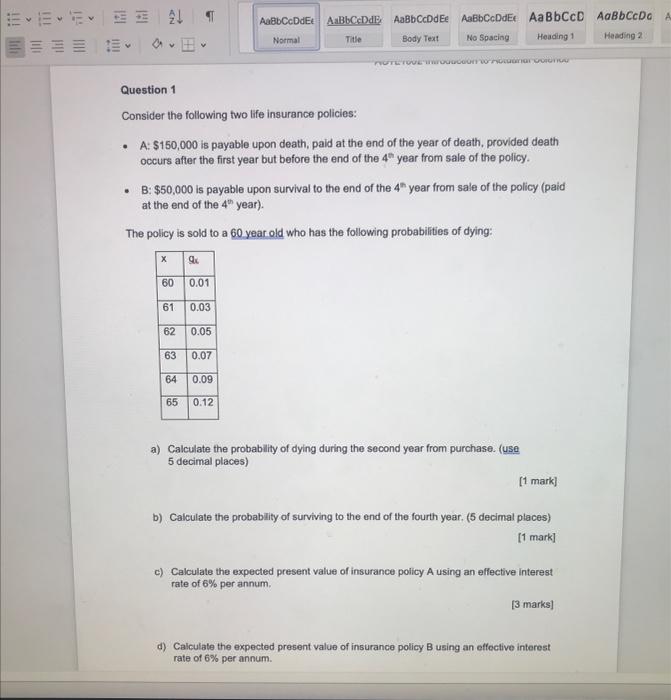
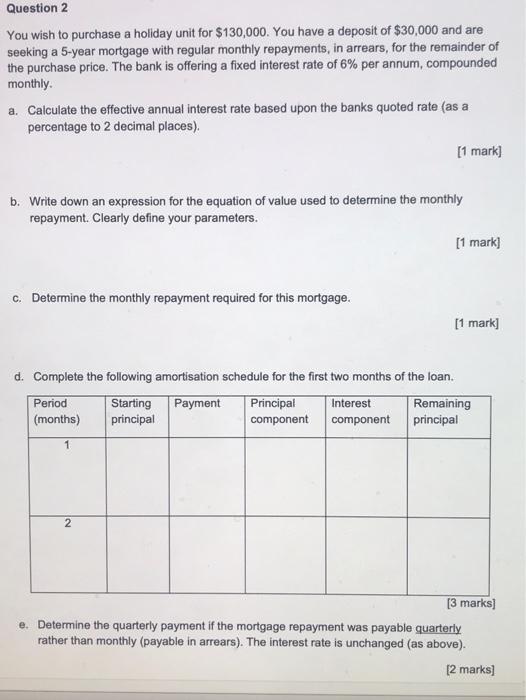
AaBb CcDdEt ABCDE AaBb CcDdee AaBbCcDdEx Aa BbCD AaBbCcDa A Normal Title Body Text No Spacing Heading 2 Heading 1 v NOT TO WOWO Question 1 Consider the following two life insurance policies: A: $150,000 is payable upon death, paid at the end of the year of death, provided death occurs after the first year but before the end of the 4h year from sale of the policy. B: $50,000 is payable upon survival to the end of the 4 year from sale of the policy (pald at the end of the 4th year). The policy is sold to a 60 year old who has the following probabilities of dying: 60 0.01 61 0.03 62 0.05 63 0.07 64 0.09 65 0.12 a) Calculate the probability of dying during the second year from purchase. (use 5 decimal places) [1 mark] b) Calculate the probability of surviving to the end of the fourth year, (5 decimal places) [1 mark] c) Calculate the expected present value of insurance policy A using an effective interest rate of 6% per annum [3 marks) d) Calculate the expected present value of insurance policy B using an effective interest rate of 6% per annum. Question 2 You wish to purchase a holiday unit for $130,000. You have a deposit of $30,000 and are seeking a 5-year mortgage with regular monthly repayments, in arrears, for the remainder of the purchase price. The bank is offering a fixed interest rate of 6% per annum, compounded monthly a. Calculate the effective annual interest rate based upon the banks quoted rate (as a percentage to 2 decimal places). [1 mark] b. Write down an expression for the equation of value used to determine the monthly repayment. Clearly define your parameters. [1 mark] c. Determine the monthly repayment required for this mortgage. [1 mark] d. Complete the following amortisation schedule for the first two months of the loan. Payment Period (months) Starting principal Principal component Interest component Remaining principal 1 2 [3 marks] e. Determine the quarterly payment if the mortgage repayment was payable quarterly rather than monthly (payable in arrears). The interest rate is unchanged (as above). [2 marks] Question 3 A company needs to raise money to expand and decides to issue a 3-year bond with a face value of $1,000 and coupon rate of 8% per annum, payable every 6-months, in arrears, for the 3 year period. a) Write down an expression for the fair market value (ie the price) of the bond at the issue date. Clearly define your parameters. [1 mark) b) Given an effective annual interest rate of 7.12% per annum, determine the price of the bond at the issue date. [2 marks] c) An investor bought the bond at issue. Two years later the effective annual interest rate has increased to 8.16% per annum and the investor decides to sell the bond. Determine the fair market value at which the investor should seek to sell the bond given the new interest rate. [2 marks] [Total: 5 marks) The retirement benefit of a defined benefit superannuation fund is defined as follows: Retirement Benefit is 10% times Final Average Salary times Years of Membership Final Average Salary means the average of your salary over the 12 months immediately before the date of calculation Years of Membership means the period from the date you joined the superannuation fund to the date of calculation, measured as years and complete months The membership details for Tom Smith are: Date of birth 25/5/1965 > Date joined fund 15/2/2000 Recent Salary History o 1/1/2018 $98,000 01/1/2019 $105,000 1/1/2020 $115,000 > On 1 January 2021, salary increased to $120,000 a. Determine Tom's 'accrued' retirement benefit as at 30 June 2021, that is, the retirement benefit payable on this date assuming the member was eligible to retire, based upon membership to the date of calculation [2 marks] The superannuation fund also allows members to join the defined contribution (accumulation) section. Under this section members nominate the death benefit amount (sum insured) they wish. The fund then charges weekly insurance premiums determined using premium rates per $1,000 sum insured. An extract of the weekly premium rate is illustrated below Age Weekly Insurance Premium per $1,000 Sum Insured 50 0.010 51 0.015 52 0.020 b. Assuming a sum insured of $100,000 which remains constant throughout, calculate the insurance premium over the full year for a member aged 50 years and 3 months at the start of the year 11 mark] Question 5 A company has a market capitalisation of $80 million and outstanding debt of $20 million. Beta for the company is 1.5, the debt cost of capital is 10% per annum and the tax rate is 30% a) Calculate the Equity Cost of Capital using the Capital Asset Pricing Model (CAPM) given the risk free rate is 2% per annum and the market premium is 5%. [1 mark) b) Calculate the Weighted Average Cost of Capital (WACC) for the company. [1 mark] The company is considering two alternate projects: A: Requires an investment of $100,000 now. In return, the company expects to receive six annual payments of $25,000 with the first payment at the end of the year of investment B: Requires an investment of $100,000 now and a further investment of $10,000 one year from now. In return, the company will receive $90,000 four years from now and another $90,000 seven years from now. c) Write down an expression for the net present value of Project A. Clearly define your parameters. [1 mark] d) Using a "hurdle rate' of 10% per annum as the effective annual interest rate, calculate the net present value of Project A. [2 marks] e) Using a "hurdle rate' of 11% per annum as the effective annual interest rate, calculate the net present value of Project B. [2 marks] 1) By comparing the net present value of each project recommend, with reasons, which project the company should undertake. [1 mark] AaBb CcDdEt ABCDE AaBb CcDdee AaBbCcDdEx Aa BbCD AaBbCcDa A Normal Title Body Text No Spacing Heading 2 Heading 1 v NOT TO WOWO Question 1 Consider the following two life insurance policies: A: $150,000 is payable upon death, paid at the end of the year of death, provided death occurs after the first year but before the end of the 4h year from sale of the policy. B: $50,000 is payable upon survival to the end of the 4 year from sale of the policy (pald at the end of the 4th year). The policy is sold to a 60 year old who has the following probabilities of dying: 60 0.01 61 0.03 62 0.05 63 0.07 64 0.09 65 0.12 a) Calculate the probability of dying during the second year from purchase. (use 5 decimal places) [1 mark] b) Calculate the probability of surviving to the end of the fourth year, (5 decimal places) [1 mark] c) Calculate the expected present value of insurance policy A using an effective interest rate of 6% per annum [3 marks) d) Calculate the expected present value of insurance policy B using an effective interest rate of 6% per annum. Question 2 You wish to purchase a holiday unit for $130,000. You have a deposit of $30,000 and are seeking a 5-year mortgage with regular monthly repayments, in arrears, for the remainder of the purchase price. The bank is offering a fixed interest rate of 6% per annum, compounded monthly a. Calculate the effective annual interest rate based upon the banks quoted rate (as a percentage to 2 decimal places). [1 mark] b. Write down an expression for the equation of value used to determine the monthly repayment. Clearly define your parameters. [1 mark] c. Determine the monthly repayment required for this mortgage. [1 mark] d. Complete the following amortisation schedule for the first two months of the loan. Payment Period (months) Starting principal Principal component Interest component Remaining principal 1 2 [3 marks] e. Determine the quarterly payment if the mortgage repayment was payable quarterly rather than monthly (payable in arrears). The interest rate is unchanged (as above). [2 marks] Question 3 A company needs to raise money to expand and decides to issue a 3-year bond with a face value of $1,000 and coupon rate of 8% per annum, payable every 6-months, in arrears, for the 3 year period. a) Write down an expression for the fair market value (ie the price) of the bond at the issue date. Clearly define your parameters. [1 mark) b) Given an effective annual interest rate of 7.12% per annum, determine the price of the bond at the issue date. [2 marks] c) An investor bought the bond at issue. Two years later the effective annual interest rate has increased to 8.16% per annum and the investor decides to sell the bond. Determine the fair market value at which the investor should seek to sell the bond given the new interest rate. [2 marks] [Total: 5 marks) The retirement benefit of a defined benefit superannuation fund is defined as follows: Retirement Benefit is 10% times Final Average Salary times Years of Membership Final Average Salary means the average of your salary over the 12 months immediately before the date of calculation Years of Membership means the period from the date you joined the superannuation fund to the date of calculation, measured as years and complete months The membership details for Tom Smith are: Date of birth 25/5/1965 > Date joined fund 15/2/2000 Recent Salary History o 1/1/2018 $98,000 01/1/2019 $105,000 1/1/2020 $115,000 > On 1 January 2021, salary increased to $120,000 a. Determine Tom's 'accrued' retirement benefit as at 30 June 2021, that is, the retirement benefit payable on this date assuming the member was eligible to retire, based upon membership to the date of calculation [2 marks] The superannuation fund also allows members to join the defined contribution (accumulation) section. Under this section members nominate the death benefit amount (sum insured) they wish. The fund then charges weekly insurance premiums determined using premium rates per $1,000 sum insured. An extract of the weekly premium rate is illustrated below Age Weekly Insurance Premium per $1,000 Sum Insured 50 0.010 51 0.015 52 0.020 b. Assuming a sum insured of $100,000 which remains constant throughout, calculate the insurance premium over the full year for a member aged 50 years and 3 months at the start of the year 11 mark] Question 5 A company has a market capitalisation of $80 million and outstanding debt of $20 million. Beta for the company is 1.5, the debt cost of capital is 10% per annum and the tax rate is 30% a) Calculate the Equity Cost of Capital using the Capital Asset Pricing Model (CAPM) given the risk free rate is 2% per annum and the market premium is 5%. [1 mark) b) Calculate the Weighted Average Cost of Capital (WACC) for the company. [1 mark] The company is considering two alternate projects: A: Requires an investment of $100,000 now. In return, the company expects to receive six annual payments of $25,000 with the first payment at the end of the year of investment B: Requires an investment of $100,000 now and a further investment of $10,000 one year from now. In return, the company will receive $90,000 four years from now and another $90,000 seven years from now. c) Write down an expression for the net present value of Project A. Clearly define your parameters. [1 mark] d) Using a "hurdle rate' of 10% per annum as the effective annual interest rate, calculate the net present value of Project A. [2 marks] e) Using a "hurdle rate' of 11% per annum as the effective annual interest rate, calculate the net present value of Project B. [2 marks] 1) By comparing the net present value of each project recommend, with reasons, which project the company should undertake. [1 mark]