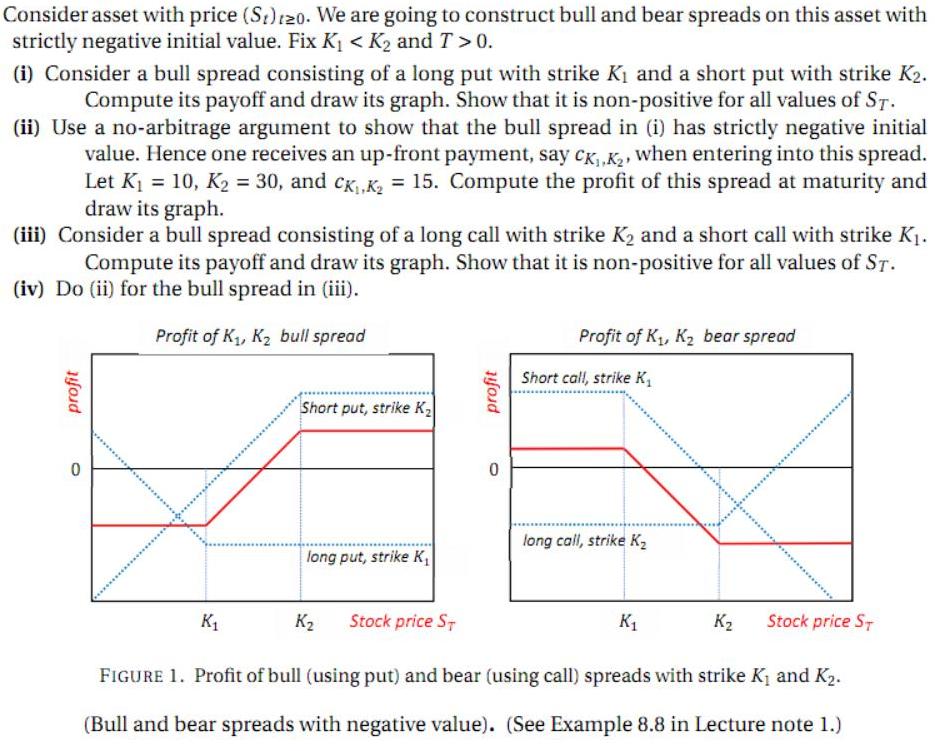
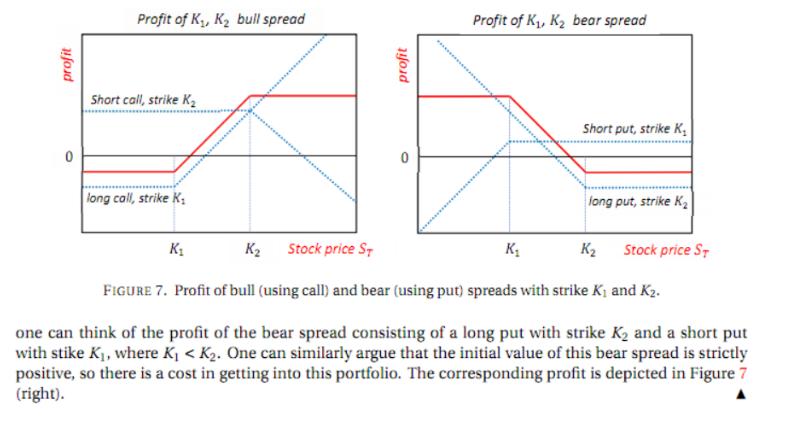
Consider asset with price (S)120. We are going to construct bull and bear spreads on this asset with strictly negative initial value. Fix K1 < K2 and T > 0. (i) Consider a bull spread consisting of a long put with strike Ki and a short put with strike K2. Compute its payoff and draw its graph. Show that it is non-positive for all values of ST. (ii) Use a no-arbitrage argument to show that the bull spread in (i) has strictly negative initial value. Hence one receives an up-front payment, say cK,,K2, when entering into this spread. Let K1 = 10, K2 = 30, and c, K, = 15. Compute the profit of this spread at maturity and %3D draw its graph. (iii) Consider a bull spread consisting of a long call with strike K2 and a short call with strike K1. Compute its payoff and draw its graph. Show that it is non-positive for all values of ST. (iv) Do (ii) for the bull spread in (iii). Profit of K, K2 bull spread Profit of K, K2 bear spread Short call, strike K, Short put, strike K2 long call, strike K2 long put, strike K, K1 K2 Stock price ST K1 K2 Stock price ST FIGURE 1. Profit of bull (using put) and bear (using call) spreads with strike K1 and K2. (Bull and bear spreads with negative value). (See Example 8.8 in Lecture note 1.) Example 8.8 (Profit of bull and bear spreads). Recall that we have discussed a bull spread using call options and a bear spread using put options and their values at maturity. Since we might be using non- equilibrium strike prices for the options, there might be costs in going long or short for different options. For instance, consider a bull spread consisting of a long call with strike 10 and short call with strike 30. The value at time t of this bull spread is C1o(t, T)- C30(t, T), which is nonnegative by Proposition 8.6. If this equals zero, then this bull spread gives an arbitrage opportunity, so it has to be strictly positive. This means that there is a cost, say c10,30 > 0, in involving into this spread. Then the profit at maturity of this bull spread is given by Cio(T, T)-C30(T, T)- C10,30 = (ST-10)-(ST-30)*-C10,30, (109) which is a random variable that takes both positive and negative values with positive probability. The profit of this bullspread as well as that of its constituent call options are shown in Figure 7 (left). Similarly, Profit of K, K2 bull spread Profit of K, K2 bear spread Short call, strike K2 Short put, strike K, iong call, strike K, iong put, strike K K2 Stock price S, K2 Stock price S, FIGURE 7. Profit of bull (using call) and bear (using put) spreads with strike K, and K2. one can think of the profit of the bear spread consisting of a long put with strike K2 and a short put with stike K1, where K, < K2. One can similarly argue that the initial value of this bear spread is strictly positive, so there is a cost in getting into this portfolio. The corresponding profit is depicted in Figure 7 (right). profit