Activity 4 - Working with Polynomial Functions and Their Graphs

Introduction

Consider the function

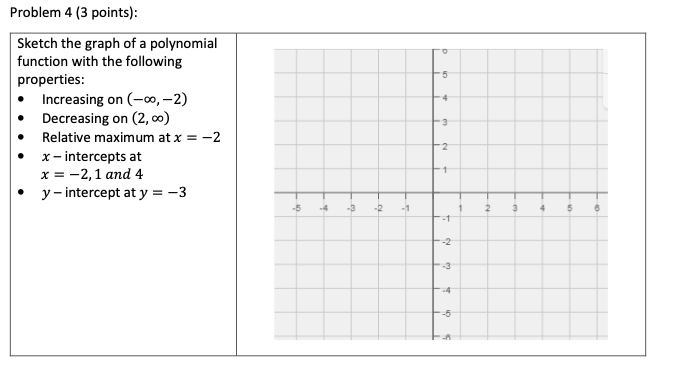
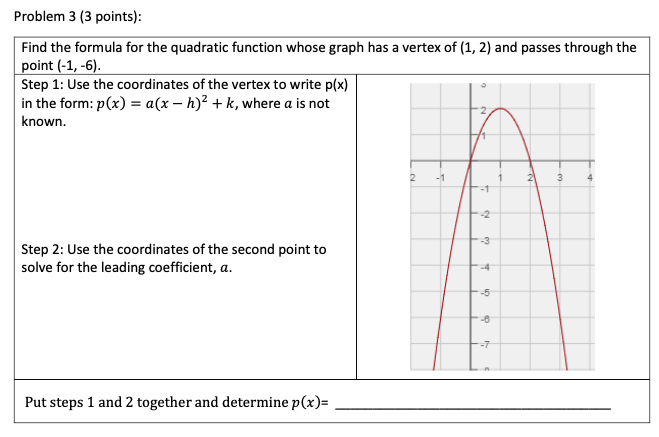
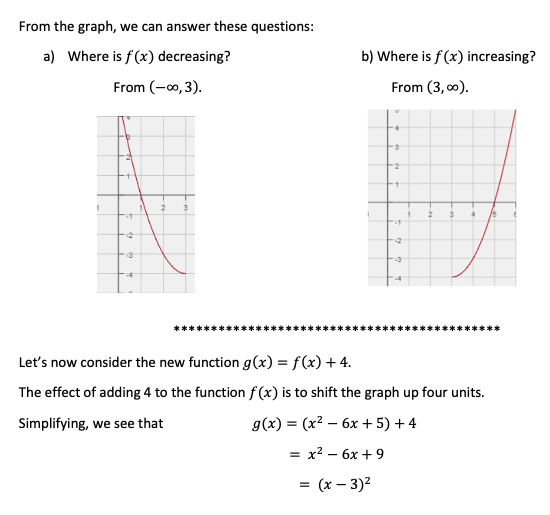
Problem 4 (3 points): Sketch the graph of a polynomial function with the following properties: Increasing on (-co, -2) Decreasing on (2, co) Relative maximum at x = -2 x - intercepts at x = -2, 1 and 4 y - intercept at y = -3 -5 -4 -3 -2 -1 2 4 5 -2 -3Problem 1 (2 points): Sketch a cubic function (third degree polynomial function) y = p(x) where p(x) > 0 on the intervals (-co, 2) and (4,6). Then determine a formula for your function. Sketch: Formula: p(x)=Problem 2 (2 points): Sketch a cubic function (third degree polynomial function) y = p(x) with two distinct zeros at x = 1 and x = 4 and a local maximum at x = 4. Then determine a formula for your function. [Hint: you will have one double root.] Sketch: Formula: p(x)=Problem 3 (3 points): Find the formula for the quadratic function whose graph has a vertex of (1, 2) and passes through the point (-1, -6). Step 1: Use the coordinates of the vertex to write p(x) in the form: p(x) = a(x - h)