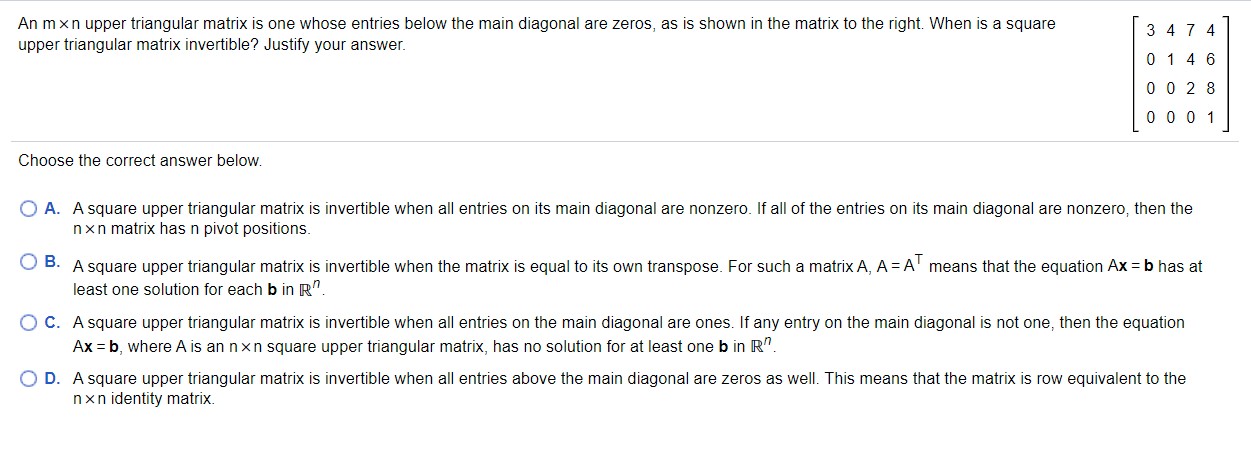
An m xn upper triangular matrix is one whose entries below the main diagonal are zeros, as is shown in the matrix to the right. When is a square 3 4 7 4 upper triangular matrix invertible? Justify your answer. 0146 0028 0001 Choose the correct answer below. 0 A. Asquare upper triangular matrix is invertible when all entries on its main diagonal are nonzero. lfall of the entries on its main diagonal are nonzero. then the n xn matrix has n pivot positions. 0 5- Asquare upper triangular matrix is invertible when the matrix is equal to its own transpose. For such a matrix A, A: AT means that the equation Ax = b has at least one solution for each b in R". O C. Asquare upper triangular matrix is invertible when all entries on the main diagonal are ones. If any entry on the main diagonal is not one, then the equation M2 b, where A is an n x n square upper triangular matrix, has no solution for at least one b in IR\". 0 D. Asquare upper triangular matrix is invertible when all entries above the main diagonal are zeros as well. This means that the matrix is row equivalent to the n x n identityr matrix