and here is exercise 12.4 for reference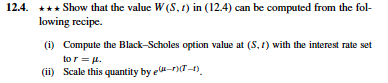and here is black-scholes formula 8.19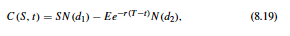

19.6. Consider the geometric average price Asian call option, with payoff 1 max ITS(i) E.0 198 Exotic options where the points lili 1 are equally spaced with t iAt and nAt T By writing ITS(i) i-1 n-2 n-1 S(2) and using the 'additive mean and variance property of independent normal random variables mentioned as item (iii) at the end of Section 35, show that for the asset model (6.9) under risk neutrality, we have 1 (n +1) (n +1) (2n 1) IT soli) log T., a (Note in particular that this establishes a ity structure, akin to that of the underlying asset.) Valuing the option as the risk-neutral discounted expected payoff, deduce that the time-zero option value is equivalent to the discounted expected payoff for a European call option whose asset has volatility satisfying 22 (n +1)(2n +1) and drift given by 2, (n 1) (r Use Exercise 124 and the Black-Scholes formula (8.19) to deduce that the time-zero geometric average price Asian call option value can be written -r T where T. 19.6. Consider the geometric average price Asian call option, with payoff 1 max ITS(i) E.0 198 Exotic options where the points lili 1 are equally spaced with t iAt and nAt T By writing ITS(i) i-1 n-2 n-1 S(2) and using the 'additive mean and variance property of independent normal random variables mentioned as item (iii) at the end of Section 35, show that for the asset model (6.9) under risk neutrality, we have 1 (n +1) (n +1) (2n 1) IT soli) log T., a (Note in particular that this establishes a ity structure, akin to that of the underlying asset.) Valuing the option as the risk-neutral discounted expected payoff, deduce that the time-zero option value is equivalent to the discounted expected payoff for a European call option whose asset has volatility satisfying 22 (n +1)(2n +1) and drift given by 2, (n 1) (r Use Exercise 124 and the Black-Scholes formula (8.19) to deduce that the time-zero geometric average price Asian call option value can be written -r T where T