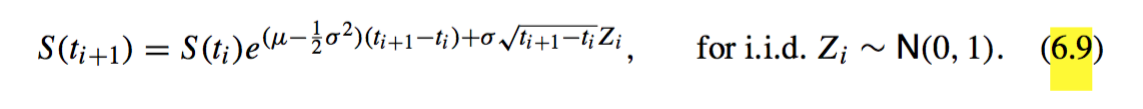
\f19,6 * * * Consider the geometric average price Asian call option, with payo n l max (H500) -E,0 , i=1 198 Exotic options where the points {t5}?=1 are equally spaced with t.- = iAt and nAt = T. By writing " _ sun) S(r,,_1) 2 San2) 3 HS\") ' 50H) (sum) (San3)) ___ (5(t3))n_2(502))n_1 (801))\" S, $02) 501) So 0 and using the 'additive mean and variance' property of independent normal random variables mentioned as item (iii) at the end of Section 3.5, show that for the asset model (6.9) under risk neutrality, we have n l 10, (11mm) /, =N(r_,az)r,azw#T). (Note in particular that this establishes a lognormality structure, akin to that of the underlying asset.) Valuing the option as the risk-neutral discounted expected payoff, deduce that the time-zero option value is equivalent to the discounted expected payoff for a European call option whose asset has volatility '8' satisfying momma-17mg 32 02 (n +1)(2n +1) _ 6:12 and drift If given by A A n+1 LL: %0'2+(r%0'2)( ). 2n Use Exercise 12.4 and the BlackScholes formula (8.19) to deduce that the timezero geometric average price Asian call option value can be written erT (SOeETNQ'i) ENG-(2)) , (19.10) where a. _103(50/E)+(+%32)T 1 3 T 1<>