Answer appropriately

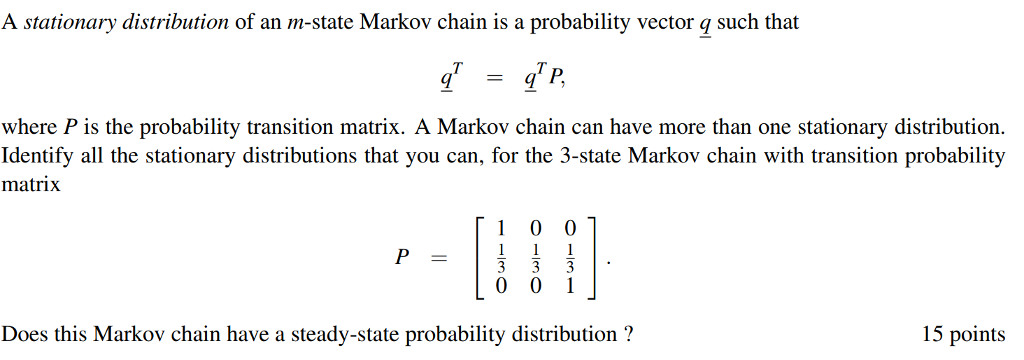
Let P be the transition matrix of a Markov chain with 7 states. Which one of the following statements is not always true? O p2 is the transition matrix of a Markov chain with 72 states. If O is another transition matrix of a Markov chain with 72 states, then PQ is the transition matrix of a Markov chain with 72 states. O If ) is another transition matrix of a Markov chain with 72 states, then *(P + Q) is the transition matrix of a Markov chain with 7, states. If P is invertible, then p-1 is the transition matrix of a Markov chain with 71, states.2. (15 pts) Consider a Markov chain { Xn } with state space S = {0, 1, 2} and transition matrix and transition matrix P = O ON/H HNIH O (1) Let the mapping f : S - S satisfy f(0) = 0 and f(2) = 1 and assume that f(1) + f(2). If Yn = f(Xn), then when is { Yn } a Markov chain? Is { Yn } always a Markov chain? In other words, are functions of Markov chains always Markov chains?Consider a standard chessboard with an 8 x 8 grid of possible locations. We define a Markov chain by randomly moving a single chess piece on this board. The initial location Xo is sampled uniformly among the 82 = 64 squares. At time t, the piece then chooses Xt+1 by sampling uniformly from the set of legal moves given its current location Xt. For a description of legal chess moves, see: http://en. wikipedia. org/wiki/Rules_of_chess#Basic_moves. a) Suppose the chess piece is a king, which can move to any of the 8 adjacent squares. Is the Markov chain irreducible? Is the Markov chain aperiodic? b) Suppose the chess piece is a bishop. Is the Markov chain irreducible? Is the Markov chain aperiodic? c) Suppose the chess piece is a knight. Is the Markov chain irreducible? Is the Markov chain aperiodic?A stationary distribution of an m-state Markov chain is a probability vector q such that = q P, where P is the probability transition matrix. A Markov chain can have more than one stationary distribution. Identify all the stationary distributions that you can, for the 3-state Markov chain with transition probability matrix O O P Owl Does this Markov chain have a steady-state probability distribution ? 15 points