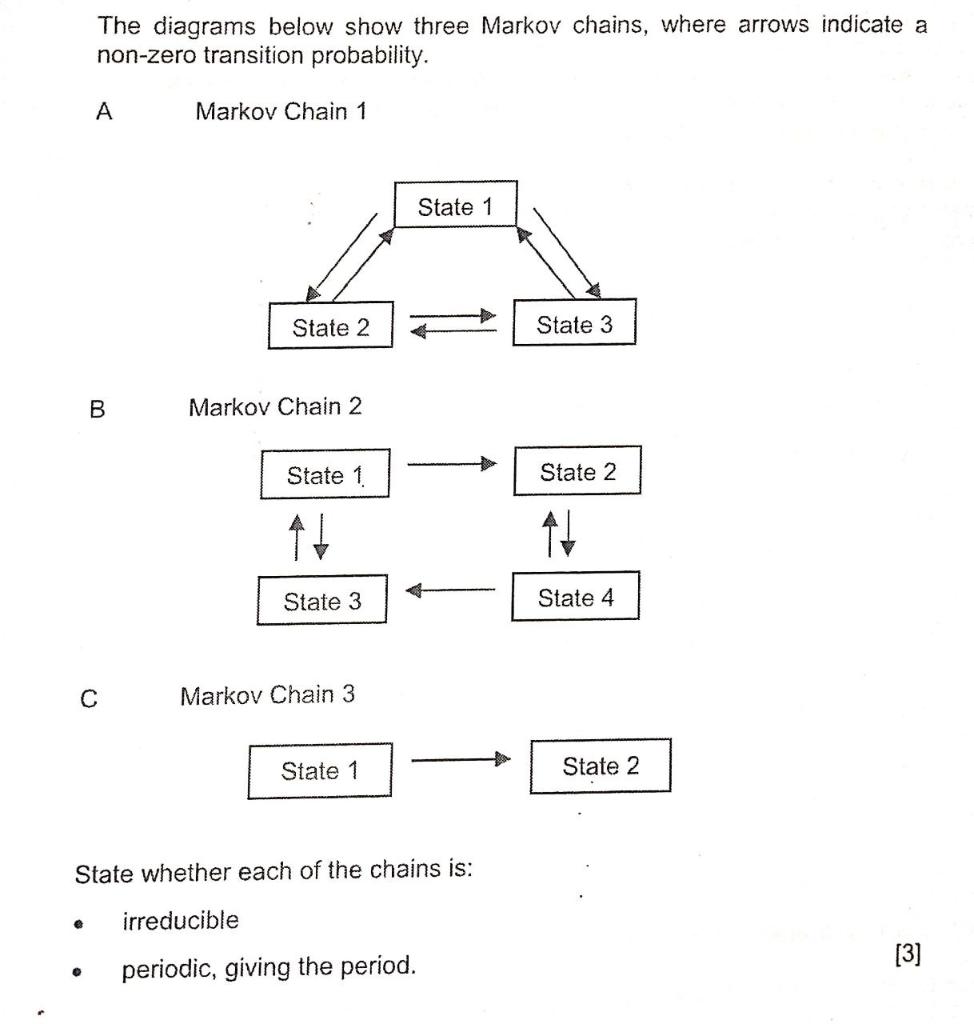
Let P be the transition matrix of a Markov chain with 7 states. Which one of the following statements is not always true? O p2 is the transition matrix of a Markov chain with 71 states. If O is another transition matrix of a Markov chain with 72 states, then PQ) is the transition matrix of a Markov chain with 71 states. O If ) is another transition matrix of a Markov chain with 72 states, then *(P + Q) is the transition matrix of a Markov chain with 7, states. If P is invertible, then p-1 is the transition matrix of a Markov chain with 71 states.4. Consider the Markov chain X = {X,} with state space S = {0, 1, 2, ...} and transition probabilities 1 ifj=i-1 Puj =1 0 otherwise , for i 2 1 and Poo = 0, Poj = for j > 1. (a) Is this Markov chain irreducible? Determine the period for every state. (b) Is the Markov chain recurrent or transient? Explain. (c) Is the Markov chain positive recurrent? If so, compute the sta- tionary probability distribution. (d) For each state i, what is the expected number of steps to return to state i if the Markov chain X starts at state i? 5. Consider a Markov chain X = {X,} with state space S = {0, 1. 2,...} and transition probability matrix 0 1 0 O 0 0 P 0 4 0 0 P = O p 0 q 0 0 . . . 0 0 P 0 4 0 Here p > 0, q > 0 and p+q = 1. Determine when the chain is positive recurrent and compute its stationary distribution.The diagrams below show three Markov chains, where arrows indicate a non-zero transition probability. A Markov Chain 1 State 1 State 2 State 3 B Markov Chain 2 State 1 State 2 State 3 State 4 C Markov Chain 3 State 1 State 2 State whether each of the chains is: e irreducible . periodic, giving the period. [3]