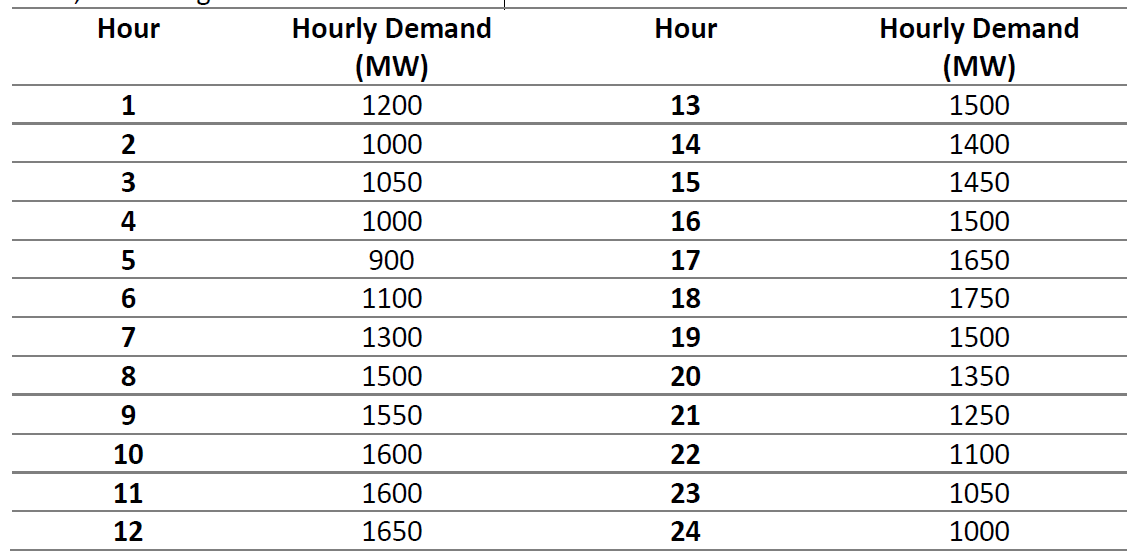
As a vertically integrated company, Georgia Power is responsible for operations of a fleet of power plants in the state of Georgia. You are a local operator, responsible for 8 power plants. All these 8 power plants have a production capacity of 220 MW (i.e. can produce up to 220MW), and a per unit production cost of 40, 34, 22 and 13 $/MWh, respectively. These power plants can produce power only if they are turned on. The cost associated with having a turned on (committed) power plant is 40$/hour for each generator. (i.e. if power plant produces 10MW in one hour, it needs to pay 40$ for turning on the power plant, and 10* 40$ for producing 10MW). The power plants are operating for a 24 hour period, and they need to satisfy a local demand in the area, which is given in the table below:

Assume that the total production from the power plants should satisfy the demand at each hour. Formulate a problem that minimizes the cost of production while satisfying the demand for each hour. (i.e. determine which power plant to turn on and how much to produce). The power plants can increase or decrease their production by at most 100MW per hour. (i.e. if power plant is producing 105 in hour 5, its production in the next time period should be between 5MW and 205MW.

Your report should include the following: Overview of the case (less than half a page) Mathematical formulation o Define decision variables. o Formulate objective function and constraints. Computer solution: Solve the problem using Xpress

* I want the Xpress results and code file as well to have in report. Thank You

\begin{tabular}{cccc} \hline Hour & Hourly Demand (MW) & Hour & Hourly Demand (MW) \\ \hline 1 & 1200 & 13 & 1500 \\ \hline 2 & 1000 & 14 & 1400 \\ \hline 3 & 1050 & 15 & 1450 \\ \hline 4 & 1000 & 16 & 1500 \\ \hline 5 & 900 & 17 & 1650 \\ \hline 6 & 1100 & 18 & 1750 \\ \hline 7 & 1300 & 19 & 1500 \\ \hline 8 & 1500 & 20 & 1350 \\ \hline 9 & 1550 & 21 & 1250 \\ \hline 10 & 1600 & 22 & 1100 \\ \hline 11 & 1600 & 23 & 1050 \\ \hline 12 & 1650 & 24 & 1000 \\ \hline \end{tabular} \begin{tabular}{cccc} \hline Hour & Hourly Demand (MW) & Hour & Hourly Demand (MW) \\ \hline 1 & 1200 & 13 & 1500 \\ \hline 2 & 1000 & 14 & 1400 \\ \hline 3 & 1050 & 15 & 1450 \\ \hline 4 & 1000 & 16 & 1500 \\ \hline 5 & 900 & 17 & 1650 \\ \hline 6 & 1100 & 18 & 1750 \\ \hline 7 & 1300 & 19 & 1500 \\ \hline 8 & 1500 & 20 & 1350 \\ \hline 9 & 1550 & 21 & 1250 \\ \hline 10 & 1600 & 22 & 1100 \\ \hline 11 & 1600 & 23 & 1050 \\ \hline 12 & 1650 & 24 & 1000 \\ \hline \end{tabular}