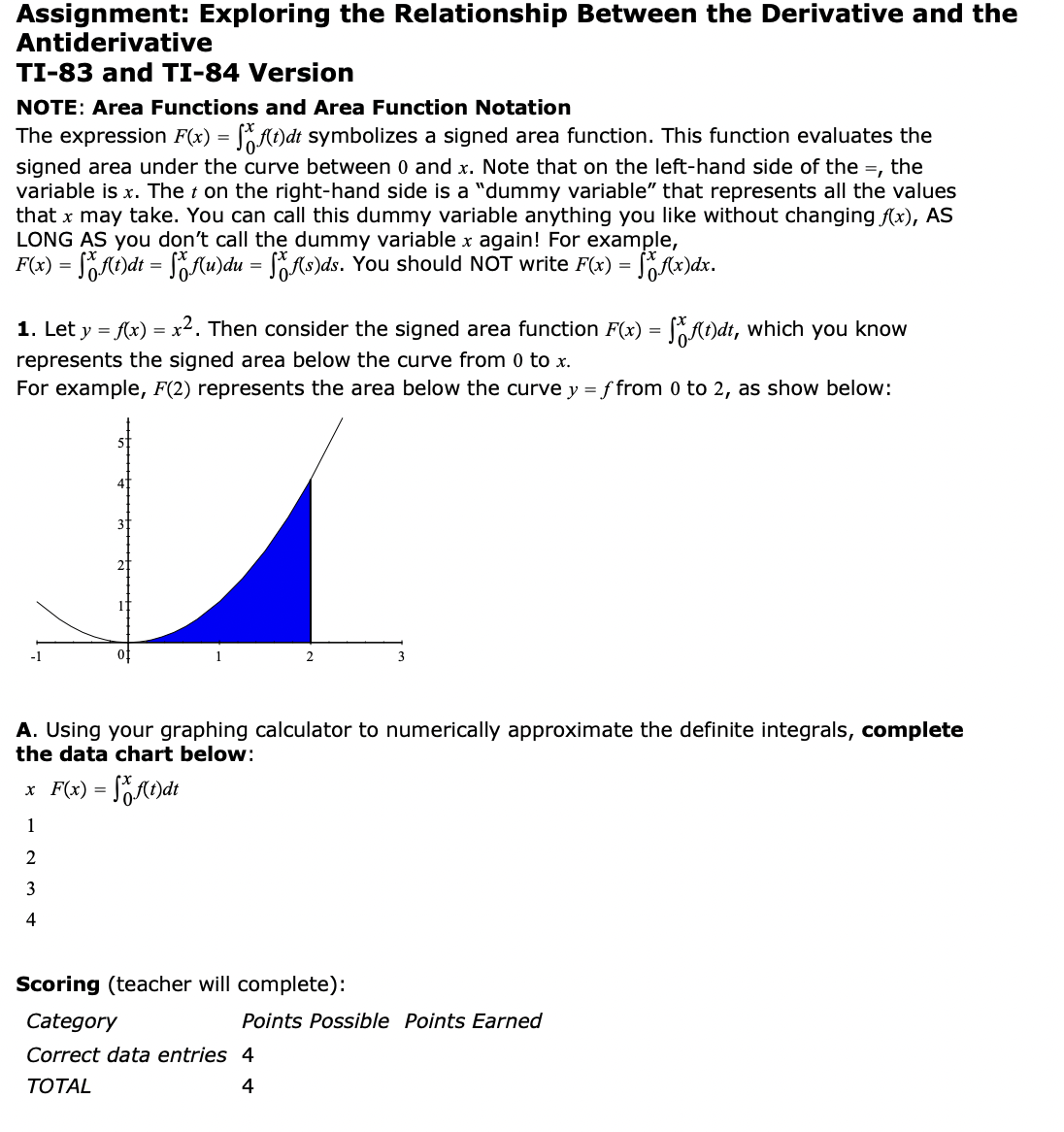
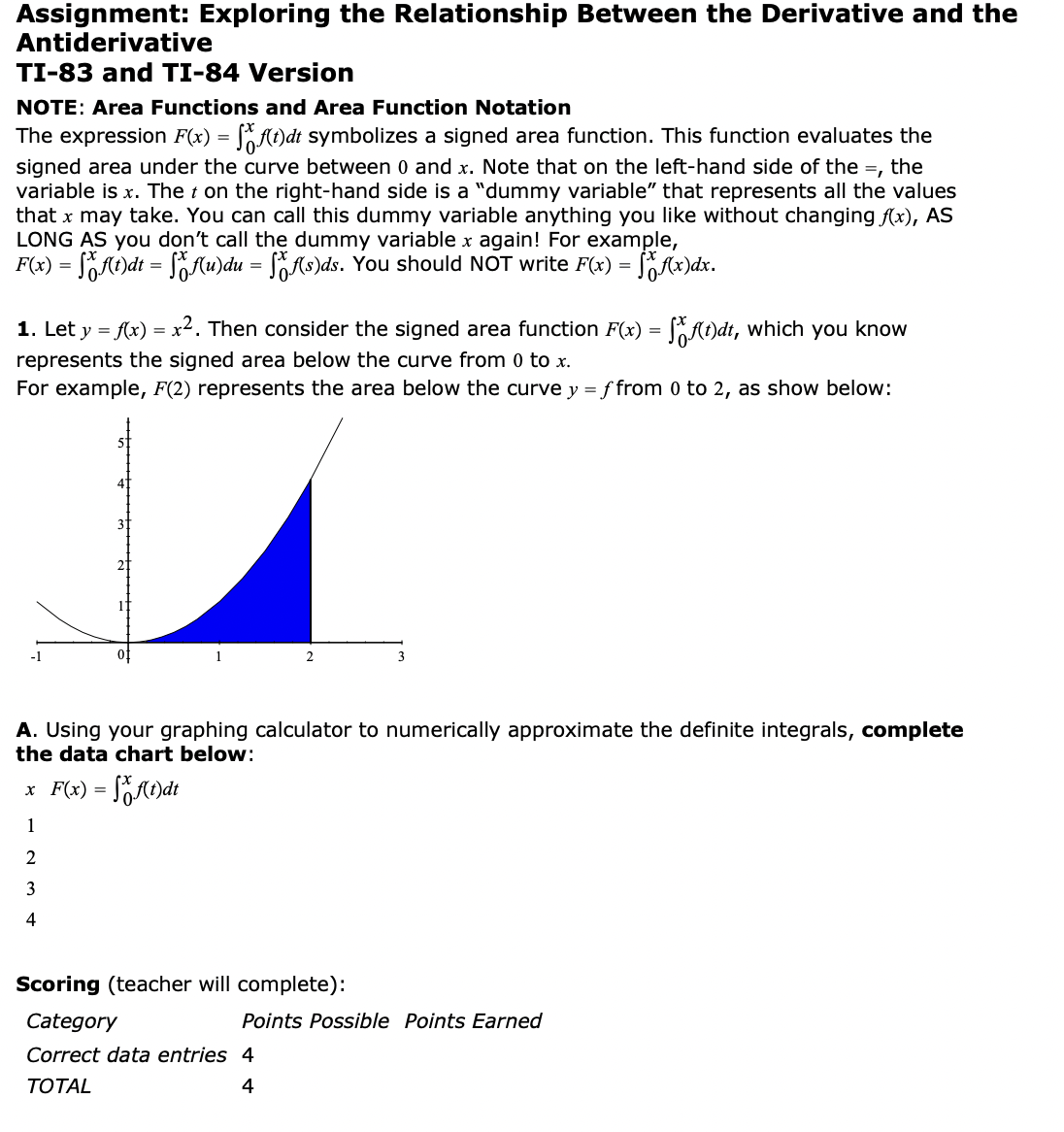
Assignment: Exploring the Relationship Between the Derivative and the Antiderivative \"-83 and TI-84 Version NOTE: Area Functions and Area Function Notation The expression F(x) = 31mm symbolizes a signed area function. This function evaluates the signed area under the curve between 0 and 1:. Note that on the lefthand side of the =, the variable is x. The t on the right-hand side is a \"dummy variable" that represents all the values that .1: may take. You can call this dummy variable anything you like without changing x), AS LONG AS you don't call the dummy variable I again! For example, m) = 3mm = 311m\" = ISsMs. You should NOT write F(x) = gxm. 1. Lety =x) = x2. Then consider the signed area function F(x) = Etr, which you know represents the signed area below the curve from 0 to I. For example, F(2) represents the area below the curve y = f from 0 to 2, as show below: A. Using your graphing calculator to numerically approximate the definite integrals, complete the data chart below: I F(x) = Ema: thil Scoring (teacher will complete): Category Points Possible Points Earned Correct data entries 4 TOTAL 4 B. Now, you'll use your calculator to create an area function F(x). By \"area function," we mean a function where you enter an .1: value, and the output is the area under the curve x) = 3:2. The function will be in the form 01:5 and will represent the area function FOE). You can do this by doing a \"regression" on your calculator; enter your data points (from the table you lled in), and your calculator will try to nd a function that matches those data points. On the TI- 83, this is done by pressing STAT|EDIT and then entering your data into the statistical register, 3: values go in L1, F(x) values go in L2. Then go STATICALClA: Pereg, which will nd a function (in the form y= axb) that ts your data points. (See pages 12- 27 in the TI- 83 book if needed. ) Remember that the calculator is approximating, so if it tells you that a = 12299999999 and b = 4200000001, it's legitimate to just take a = 123 and b = 12. Your function approximating F(x) is: Scoring (teacher will complete): Category Points Possibie Points Earned Your equation for F(x) of the form axb 4 TOTAL 4 C. What is the relationship between your function approximating F(x) and the antiderivative of x) = x2; how are they similar and how are they different? Scoring (teacher will complete): Category Points Possibie Points Earned Correct reiationsbip between F(x) and the antiderivative of x) 3 TOTAL 3 D. Using the relationship you just described above and taking 10:) = 4x3 + 12x2 +2x, take a guess at an equation for the function F(x)= ftedr, the signed area function for f In other words, ta3ke a gluess- at an area function that will give the area under the curve x)= 3+ 121: Your4 guess. F(x) = 311er = Scoring (teacher will complete): Category Points Possibie Points Earned Your guess for F(x) 2 TOTAL 2 E. Now, using your formula for F(x) (your guess in part D) and your calculator to numerically approximate the definite integrals, complete the table below, and discuss whether your formula for F(x) seems to work. x of()dt ( calculator approximation) Your F(x) W N Scoring (teacher will complete): Category Points Possible Points Earned Data - chart 3 Discussion 2 TOTAL F. Based on your work, can you draw any general conclusions concerning functions f(x) and signed area functions (definite integrals) of()di and how they relate? Even if you can't, say something about what your work signifies. Scoring (teacher will complete): Category Points Possible Points Earned Any thoughtful comment 2 TOTAL N