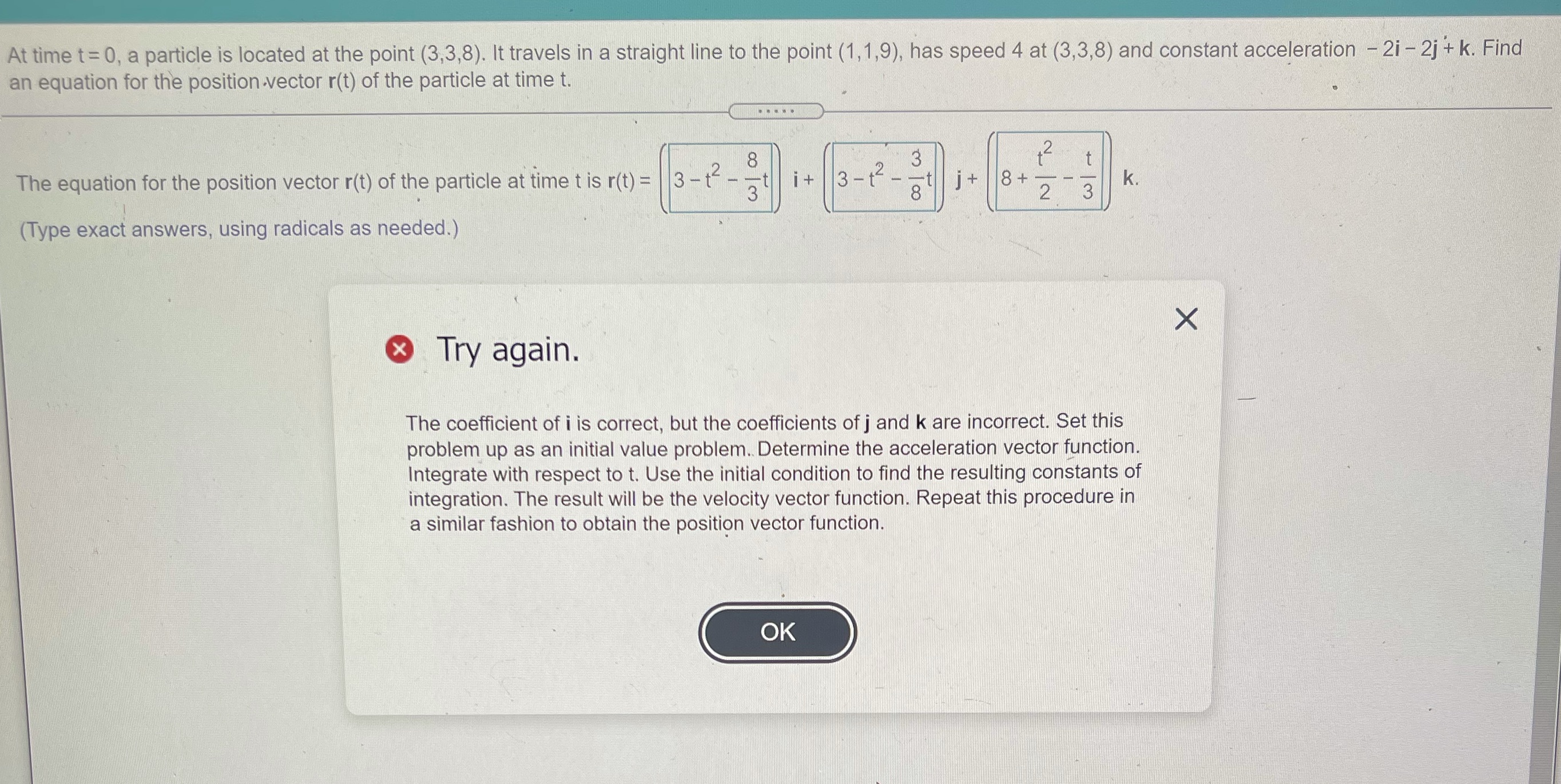
At time t= 0, a particle is located at the point (3,3,8). It travels in a straight line to the point (1, 1,9), has speed 4 at (3,3,8) and constant acceleration - 2i - 2j + k. Find an equation for the position .vector r(t) of the particle at time t. . . . . . The equation for the position vector r(t) of the particle at time t is r(t) = 3 - + 2 it 3 - 1 + 8+ K. 3 8 2 3 (Type exact answers, using radicals as needed.) X Try again. The coefficient of i is correct, but the coefficients of j and k are incorrect. Set this problem up as an initial value problem. Determine the acceleration vector function. Integrate with respect to t. Use the initial condition to find the resulting constants of integration. The result will be the velocity vector function. Repeat this procedure in a similar fashion to obtain the position vector function. OK