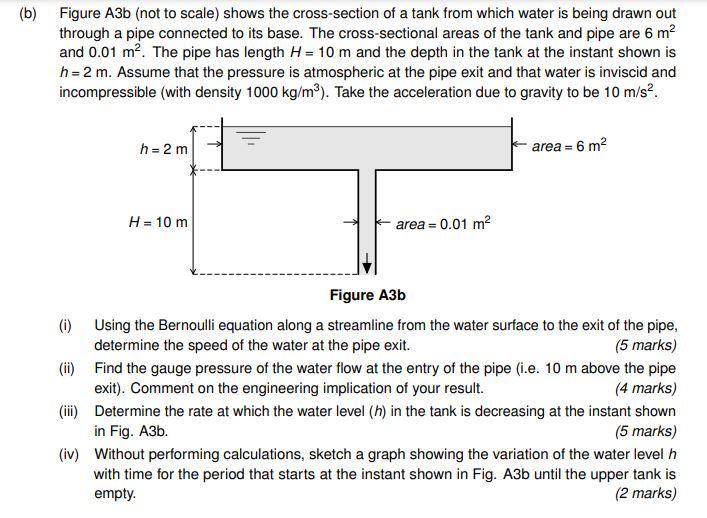
$($b$)$ Figure A$3$b $($not to scale$)$ shows the cross$-$section of a tank from which water is being drawn out through a pipe connected to its base. The cross$-$sectional areas of the tank and pipe are $\backslash (6\backslash$mathrm$\{$~m$\}^\{2\}\backslash )$ and $\backslash (0\mathrm{.}01\backslash$mathrm$\{$~m$\}^\{2\}\backslash ).$ The pipe has length $\backslash ($ H$=10\backslash$mathrm$\{$~m$\}\backslash )$ and the depth in the tank at the instant shown is $\backslash ($ h$=2\backslash$mathrm$\{$~m$\}\backslash ).$ Assume that the pressure is atmospheric at the pipe exit and that water is inviscid and incompressible $($with density $\backslash (1000\backslash$mathrm$\{$~kg$\}/\backslash$mathrm$\{$m$\}^\{3\}\backslash )).$ Take the acceleration due to gravity to be $\backslash (10\backslash$mathrm$\{$~m$\}/\backslash$mathrm$\{$s$\}^\{2\}\backslash ).$

Figure A$3$b

$($i$)$ Using the Bernoulli equation along a streamline from the water surface to the exit of the pipe, determine the speed of the water at the pipe exit.

$(5$ marks$)$

$($ii$)$ Find the gauge pressure of the water flow at the entry of the pipe $($i$.$e$.10$ m above the pipe exit$).$ Comment on the engineering implication of your result.

$(4$ marks$)$

$($iii$)$ Determine the rate at which the water level $(\backslash ($ h $\backslash ))$ in the tank is decreasing at the instant shown in Fig. A$3$b$.$

$(5$ marks$)$

$($iv$)$ Without performing calculations, sketch a graph showing the variation of the water level $\backslash ($ h $\backslash )$ with time for the period that starts at the instant shown in Fig. A$3$b until the upper tank is empty.

$(2$ marks$)$