b) We are interested in estimating and constructing a confidence interval

for the percentage change in price when a 200-square-foot bedroom is

added to a house. How can you construct this confidence interval?

What assumptions are needed to do so? State all assumptions and ex-

plain why you need the assumptions. Calculate the estimates and con-

fidence interval, and interpret them.

(c) In order to construct a confidence interval we need to estimate a stan-

dard error for the estimate in part (b). Provide the way to estimate the

standard error using another multiple regression model (Hint: Define a

parameter which represents the above estimator (in part (b)). Then one

can estimate a standard error using this relationship with another multi-

ple regression model). Based on the estimated standard error, construct

a 95% confidence interval.

(d) Suppose now u does not follow normal distribution any more. Elabo-

rate how can you calculate the confidence interval in (b) and (c). And

calculate such confidence interval using R.

3. Suppose that the model

pctstck = ?0 + ?1funds + ?2risktol + u,

satisfies the first four Gauss-Markov assumptions, where pctstck is the per-

centage of a worker's pension invested in the stock market, funds is the num-

ber of mutual funds that the worker can choose from, and risktol is some

measure of risk tolerance (larger risktol means the person has a higher tol-

erance for risk). If funds and risktol are positively correlated, what are the

bias and inconsistency in ??

1, the slope coefficient in the simple regression of

pctstck on funds? Moreover, how do you interpret the estimates you obtain

from this simple regression? [You SHOULD answer these questions crystal

clear.]

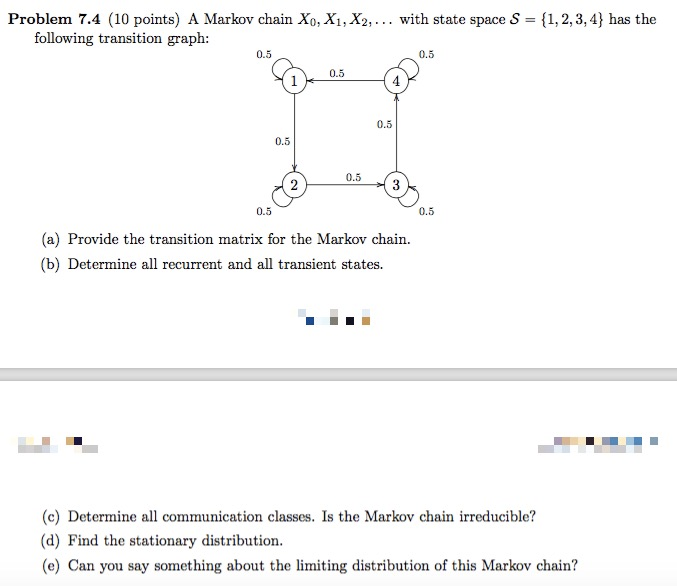
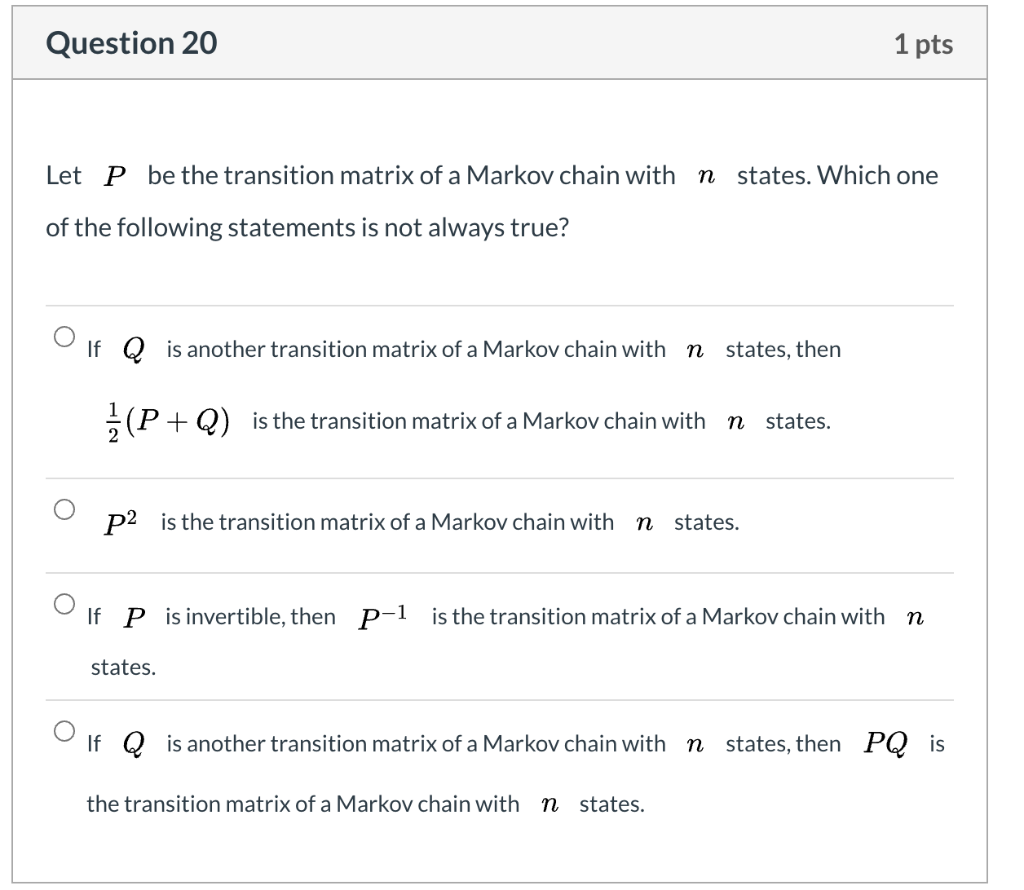
Problem 7.4 (10 points) A Markov chain Xo, X1, X2, ... with state space S = {1, 2,3, 4) has the following transition graph: 0.5 0.5 0.5 1 0.5 0.5 0.5 2 0.5 0.5 (a) Provide the transition matrix for the Markov chain. (b) Determine all recurrent and all transient states. (c) Determine all communication classes. Is the Markov chain irreducible? (d) Find the stationary distribution. (e) Can you say something about the limiting distribution of this Markov chain?Question 20 1 pts Let P be the transition matrix of a Markov chain with n states. Which one of the following statements is not always true? If Q is another transition matrix of a Markov chain with n states, then =(P + Q) is the transition matrix of a Markov chain with n states. O P2 is the transition matrix of a Markov chain with n states. If P is invertible, then p-1 is the transition matrix of a Markov chain with n states. If Q is another transition matrix of a Markov chain with n states, then PQ is the transition matrix of a Markov chain with n states.Consider a standard chessboard with an 8 x 8 grid of possible locations. We define a Markov chain by randomly moving a single chess piece on this board. The initial location Xo is sampled uniformly among the 82 = 64 squares. At time t, the piece then chooses Xt+1 by sampling uniformly from the set of legal moves given its current location Xt. For a description of legal chess moves, see: http://en. wikipedia. org/wiki/Rules_of_chess#Basic_moves. a) Suppose the chess piece is a king, which can move to any of the 8 adjacent squares. Is the Markov chain irreducible? Is the Markov chain aperiodic? b) Suppose the chess piece is a bishop. Is the Markov chain irreducible? Is the Markov chain aperiodic? c) Suppose the chess piece is a knight. Is the Markov chain irreducible? Is the Markov chain aperiodic