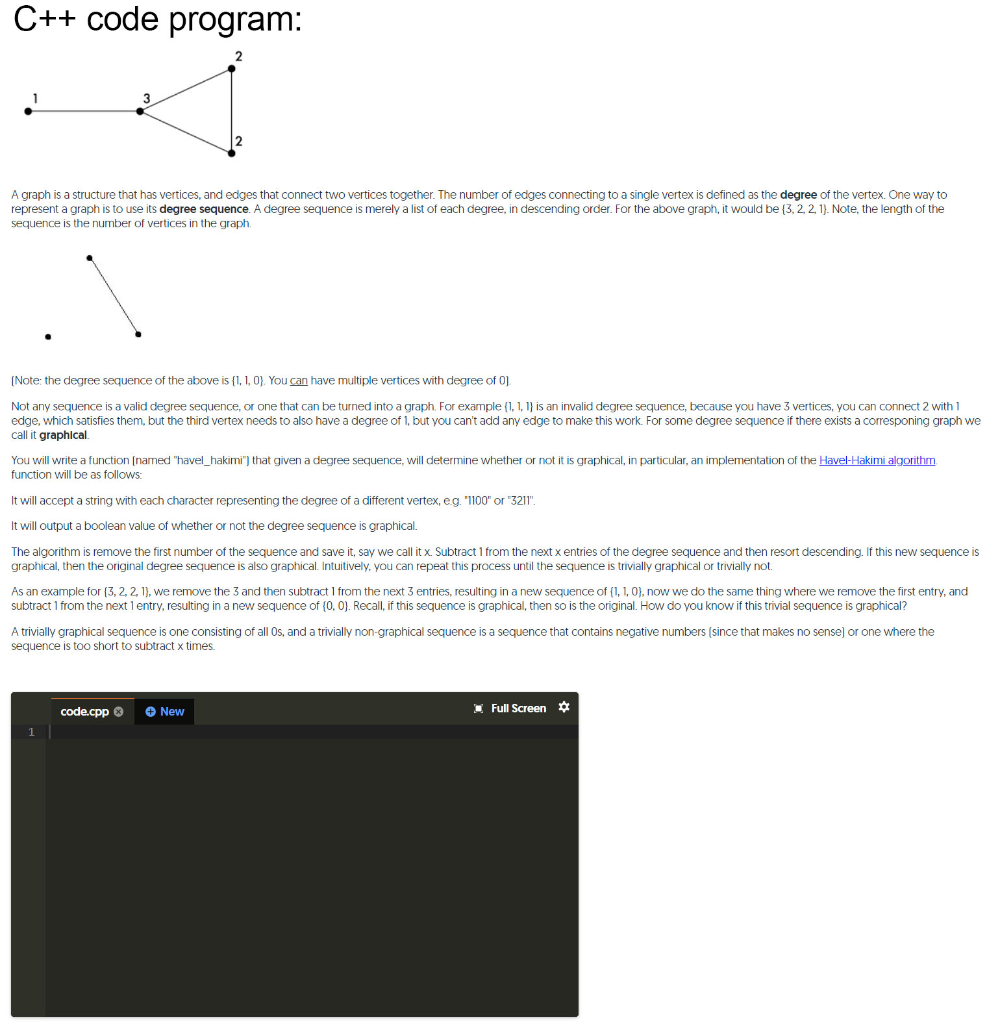
C++ code program: A graph is a structure that has vertices, and edges that connect two vertices together. The number of edges connecting to a single vertex is defined as the degree of the vertex. One way to represent a graph is to use its degree sequence. A degree sequence is merely a list of each degree, in descending order. For the above graph, it would be {3,2,2,1). Note, the length of the sequence is the number of vertices in the graph. [Note: the degree sequence of the above is {1, 1, 0). You can have multiple vertices with degree of 0] Not any sequence is a valid degree sequence, or one that can be turned into a graph. For example {1, 1, 1} is an invalid degree sequence, because you have 3 vertices, you can connect 2 with 1 edge, which satisfies them, but the third vertex needs to also have a degree of 1, but you can't add any edge to make this work. For some degree sequence if there exists a corresponing graph we call it graphical You will write a function (named "havel_hakimi") that given a degree sequence, will determine whether or not it is graphical, in particular, an implementation of the Havel-Hakimi algorithm function will be as follows: It will accept a string with each character representing the degree of a different vertex, eg, "1100" or "3211". It will output a boolean value of whether or not the degree sequence is graphical. The algorithm is remove the first number of the sequence and save it, say we call it x. Subtract 1 from the next x entries of the degree sequence and then resort descending. If this new sequence is graphical, then the original degree sequence is also graphical. Intuitively, you can repeat this process until the sequence is trivially graphical or trivially not. As an example for {3, 2, 2, 1), we remove the 3 and then subtract 1 from the next 3 entries, resulting in a new sequence of (1, 1, 0), now we do the same thing where we remove the first entry, and subtract 1 from the next 1 entry, resulting in a new sequence of (0,0). Recall, if this sequence is graphical, then so is the original. How do you know if this trivial sequence is graphical? A trivially graphical sequence is one consisting of all Os, and a trivially non-graphical sequence is a sequence that contains negative numbers (since that makes no sense) or one where the sequence is too short to subtract x times. code.cpp New Full Screen