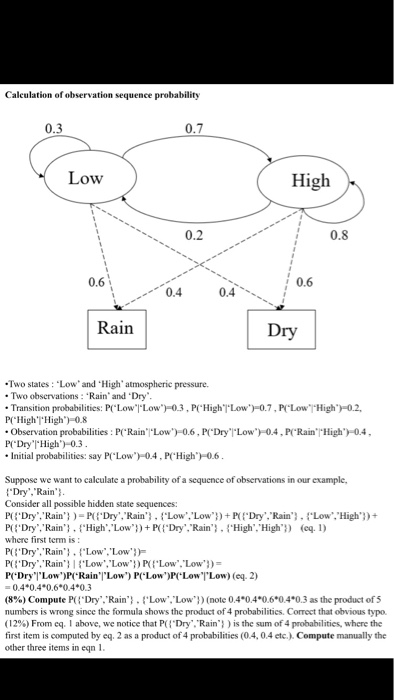
Calculation of observation sequence probability 0.3 0.7 High Low 0.8 0.6 0.6 0.4 0.4 Rain Dry Two states: Low and 'High' atmospheric pressure. Two observations: 'Rain and Dry . Transition probabilities: PCLowrLow")-0.3 , P(HighTLow.) 0.7PCLow"High')-02, P( High'l High')-0.8 Observation probabilities: P( Rain Low) 0.6, P( Dry'l Low)0.4, P Rain' High) 0.4 P(DrylHigh)-0.3 Initial probabilities: say P( Low) 0.4,P( High)0.6 Suppose we want to calculate a probability of a sequence of observations in our example, Dry'.'Rain Consider all possible hidden state sequences: PDry Rain)-PDry.'Rain', Low, Low+PDry. Rain. Low. High')+ PDry. Rain' High'. LowDry'Rain. High. High (eq. 1) where first term is PDry. Rain'Low.'Low 0.4 0.4 0.6 04 0.3 (8%) Compute PU' Dry,'Rain, } - { . Low.,Low" } ) (note 0.4.0.4*0.6.0.4193 as the product of 5 numbers is wrong since the formula shows the product of 4 probabilitics. Correct that obvious typo (12%) From eq. I above, we notice that PG, Dry:Rain'} ) is the sum of 4 probabilities, where the first item is computed by eq. 2 as a product of 4 probabilities (0.4, 0.4 etc.) Compute manually the other three items in eqn1