Question: Calculus (4.3 & 4.4) 1. -6 -4 -3 -0 -1 4 The function graphed above is: Increasing on the interval(s) Decreasing on the interval(s)Mark the


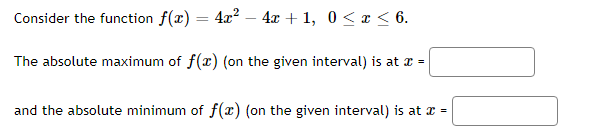
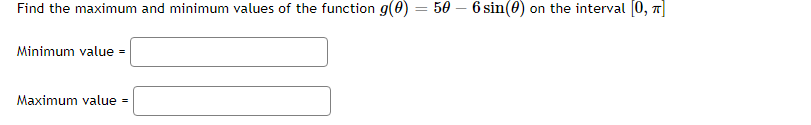



![A = C] At a: = A, does x} have a local](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6676b18b10f6b_7306676b18af3c66.jpg)
Calculus (4.3 & 4.4)
1.
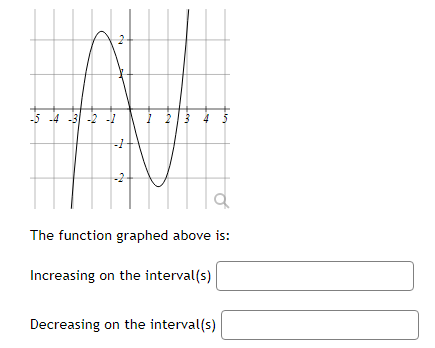
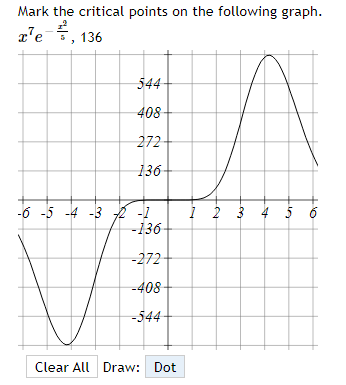
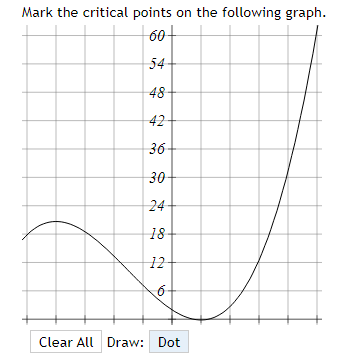
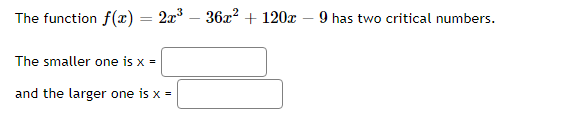


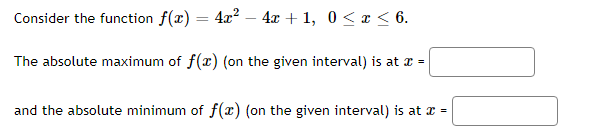
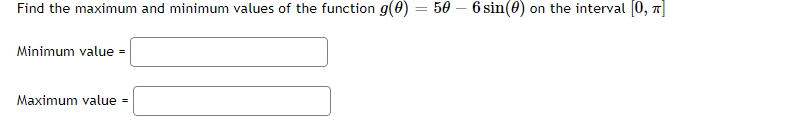




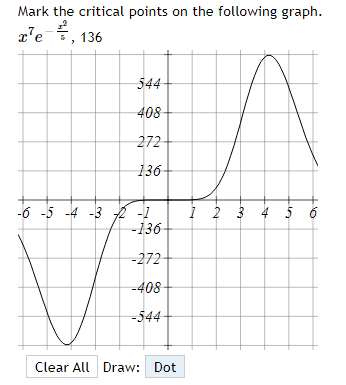
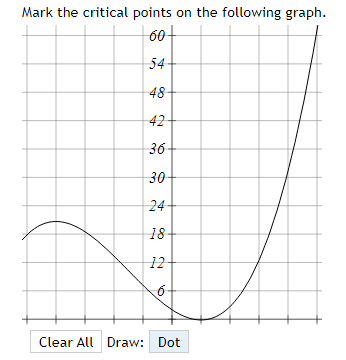
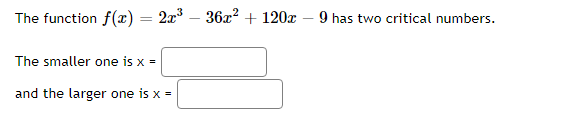
-6 -4 -3 -0 -1 4 The function graphed above is: Increasing on the interval(s) Decreasing on the interval(s)Mark the critical points on the following graph. r'e , 136 544 408 272 136 6 -5 -4 -3 4 136 -272 -408 -544 Clear All Draw: DotMark the critical points on the following graph. 60- 54 48 42 36 30 24 18 12 6 Clear All Draw: DotThe function f(x) = 2x -36x- + 120x - 9 has two critical numbers. The smaller one is x = and the larger one is x =Consider the function f[.":) = 3:2 + 4:: 2. IL?) has a critical point at I = A. Find the value of A: A = C] At a: = A, does x} have a local min, a local max, or neither? Type in 1your answer as LMIN, LMAX, or NEITHER. [:1 Consider the function f(x) = 1 -20', - 3
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


