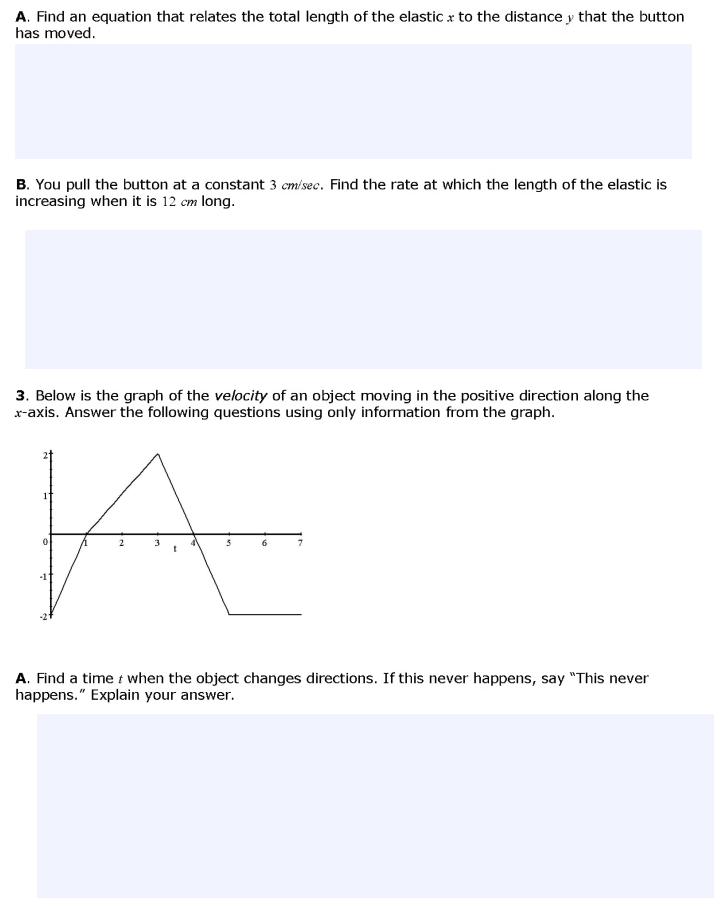
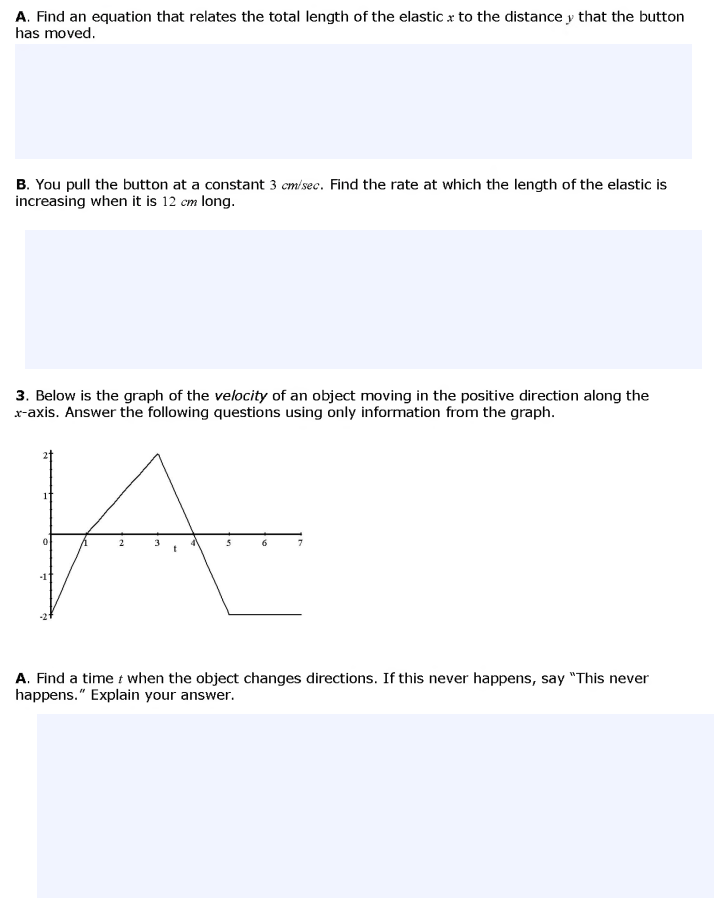
Calculus AB Assignment Applications of the Derivative 1. A candy company needs a custom box for their truffles. The box they've chosen is in the shape of a Iinder with a hemisphere of the same radius on top. The total volume of the box is I' if}? +2tr2 rjv- H ,wherey is the height of the box and 1' Is the radius of the box. .' l. Originally, the candy box was designed to have a height ofti inches and a radius of: inches. out the shipper suggests that the boxes be made slightly shorter. You now need to adjust the radius so that the height is reduced to 5.?5 inches but the volume remains constant. A. Find the value of 35% at the point r = 2, y = 15. B. Use your value of g\": to approximate the new radius for these boxes. 2. A piece of elastic is attached to two nails on a fiat board, as shown in the picture, with a button attached to the midpoint of the elastic. The nails are 5 cm apart. You stretch the elastic by pulling the button along the board in a direction that is perpendicularto the line between the nails. A. Find an equation that relates the total length of the elastic .r to the distance y that the button has moved. B. You pull the button at a constant 3 cmr'sec. Find the rate at which the length of the elastic is increasing when it is 12 cm long. 3. Below is the graph of the velocity of an object moving in the positive direction along the xaxis. Answer the following questions using only information from the graph. A. Find a time t when the object changes directions. If this never happens, say \"This never happens." Explain your answer. B. Find the time when the object is furthest to the right. Explain your answer. C. What is the object's maximum acceleration? Explain how you found this. D. What is the object's maximum speed? At what time(s) does it reach its maximum speed? 4. A forest fire is burning in a valley. Officials estimate that if the fire burns for h hours, the cost of the lost timber is 1000 dollars. They estimate that x firefighters can stop the fire in 3600 hours. The cost for each firefighter is $20 (for transportation) plus $25 per hour (for salary, meals, and other overhead). A. Let C be the cost of the fire (including the cost of the firefighters and the lost timber). C will depend on both h (how many hours the fire burns) and x (the number of firefighters sent to fight it). Give a formula for C in terms of x and h.B. Give a formula that relates x and h. C. How many firefighters should be used if the cost C of the fire is to be minimized? Justify your solution. 5. Let g be the function given by g(x) = x4 - 4x3 + 6x2 - 4x + k, where & is a constant. A. On what intervals is g increasing? Justify your answer. B. On what intervals is g concave upward? Justify your answer.C. Find the value of & for which g has 5 as its relative minimum. Justify your answer. 6. At a certain instant, the base of a triangle is 5 inches and is increasing at the rate of 1 inch per minute. At the same instant, the height is 10 inches and is decreasing at the rate of 2.5 inches per minute. Is the area of the triangle increasing or decreasing? Justify your