Can i get help with this discrete structure question?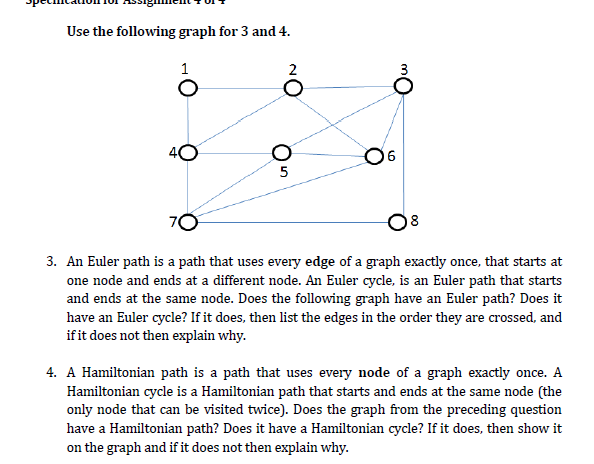

Use the following graph for 3 and 4. An Euler path is a path that uses every edge of a graph exactly once, that starts at one node and ends at a different node. An Euler cycle, is an Euler path that starts and ends at the same node. Does the following graph have an Euler path? Does it have an Euler cycle? If it does, then list the edges in the order they are crossed, and if it does not then explain why. A Hamiltonian path is a path that uses every node of a graph exactly once. A Hamiltonian cycle is a Hamiltonian path that starts and ends at the same node (the only node that can be visited twice). Does the graph from the preceding question have a Hamiltonian path? Does it have a Hamiltonian cycle? If it does, then show it on the graph and if it does not then explain why