Can I please get some help with this bungee problem?

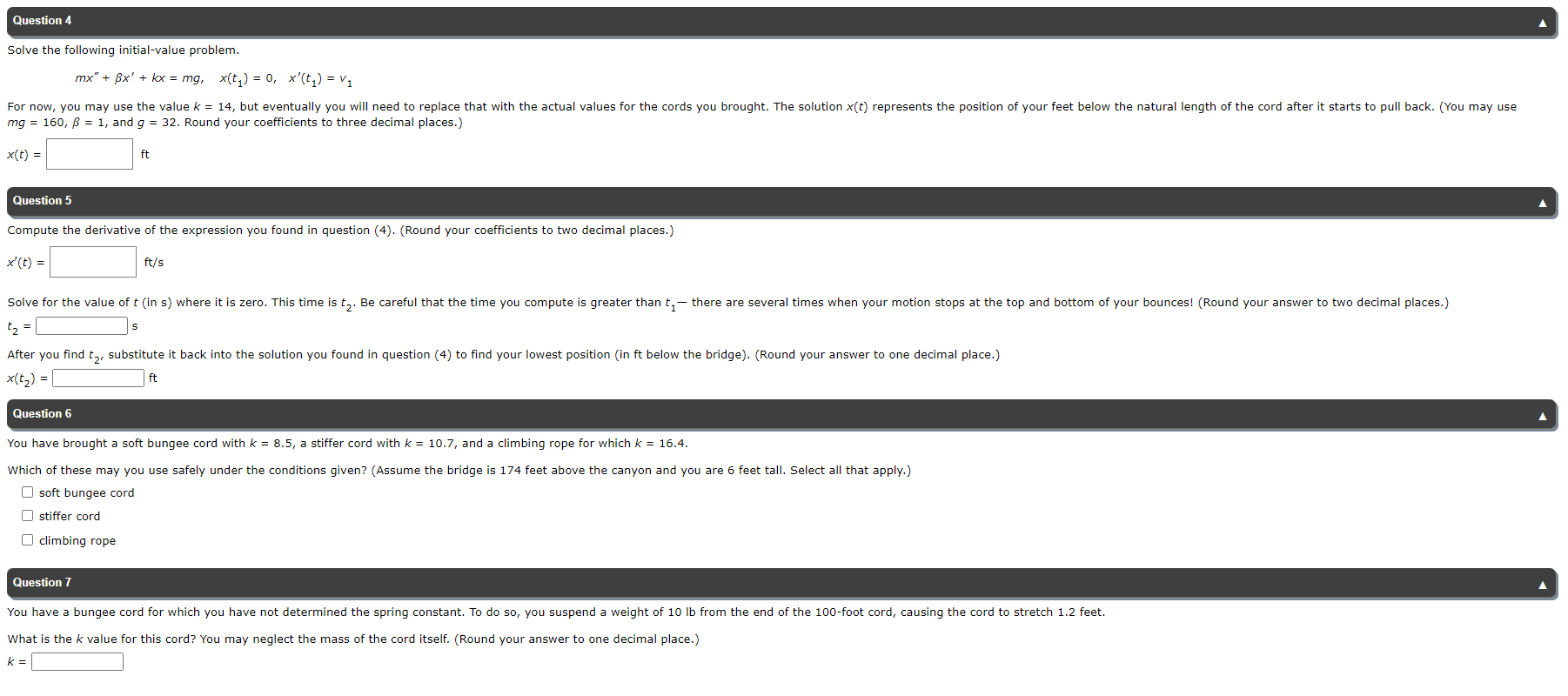
Question 4 Solve the following initial-value problem. mx + Bx'+ kx = mg, x(t, ) = 0, x'(t, ) = v1 For now, you may use the value k = 14, but eventually you will need to replace that with the actual values for the cords you brought. The solution x(t) represents the position of your feet below the natural length of the cord after it starts to pull back. (You may use mg = 160, B = 1, and g = 32. Round your coefficients to three decimal places.) x (t) = ft Question 5 Compute the derivative of the expression you found in question (4). (Round your coefficients to two decimal places.) x' (t) = it/s Solve for the value of t (in s) where it is zero. This time is t2. Be careful that the time you compute is greater than t, - there are several times when your motion stops at the top and bottom of your bounces! (Round your answer to two decimal places.) t2 = After you find t,, substitute it back into the solution you found in question (4) to find your lowest position (in ft below the bridge). (Round your answer to one decimal place.) * (t2) = ft Question 6 You have brought a soft bungee cord with k = 8.5, a stiffer cord with k = 10.7, and a climbing rope for which k = 16.4. Which of these may you use safely under the conditions given? (Assume the bridge is 174 feet above the canyon and you are 6 feet tall. Select all that apply.) O soft bungee cord O stiffer cord O climbing rope Question 7 You have a bungee cord for which you have not determined the spring constant. To do so, you suspend a weight of 10 lb from the end of the 100-foot cord, causing the cord to stretch 1.2 feet. What is the k value for this cord? You may neglect the mass of the cord itself. (Round your answer to one decimal place.) K =