Question: Can someone help me with this problem? Please explain a little bit after answering each part, thanks. [Space of polynomials P, l+2+2ptsl Let P,1 be
Can someone help me with this problem? Please explain a little bit after answering each part, thanks.

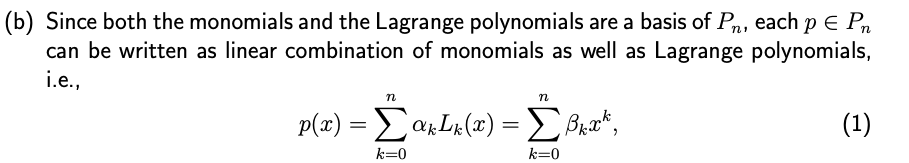
![be the space of functions defined on [1,1] that can be described](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/671362574c81f_60767136257150fe.jpg)
[Space of polynomials P,\" l+2+2ptsl Let P,1 be the space of functions defined on [1,1] that can be described by polynomials of degree less of equal to n with coefficients in R. P\" is a linear Space in the sense of linear algebra, in particular, for p,q E R, and a E R, also 3) + q and up are in P\"- Since the monomials {1,33, :32, . . . ,m\"} are a basis for P\(b) Since both the monomials and the Lagrange polynomials are a basis of Pn, each p E Pn can be written as linear combination of monomials as well as Lagrange polynomials, i.e ., n n p(a) = OK LK (20 ) = BRack, (1) k=0 *=0with appropriate coefficients am ,Bk E R. As you know from basic matrix theory, there exists a basis transformation matrix that converts the coefficients a = (an, . . . ,orn)T to the coefficients )3 = [130,\" . ,n)T. Show that this basis transformation matrix is given by the so-called Vandennonde matrix V E Ronn'l'l given by 2 .. . n1 n 1 In IID ICI 1 $0 1 I1 I2 - - - In' I" 1 1 1 V = : : : -. : : ' 2 _ . _ 111 11. 1 In In In In i.e., the relation between a and ,8 in (1) is given by a = V. An easy way to see this is to choose appropriate I in (1). (c) Note that since V transforms one basis into another basis, it must be an invertible matrix. Let us compute the condition number of V numerically.2 Compute the 2- based condition number H207) for n = 5,10, 20, 30 with uniformly spaced nodes {531 = 1 + {21)fn 1; = 0, ...,n. Based on the condition numbers, can this basis transformation be performed accurately
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


