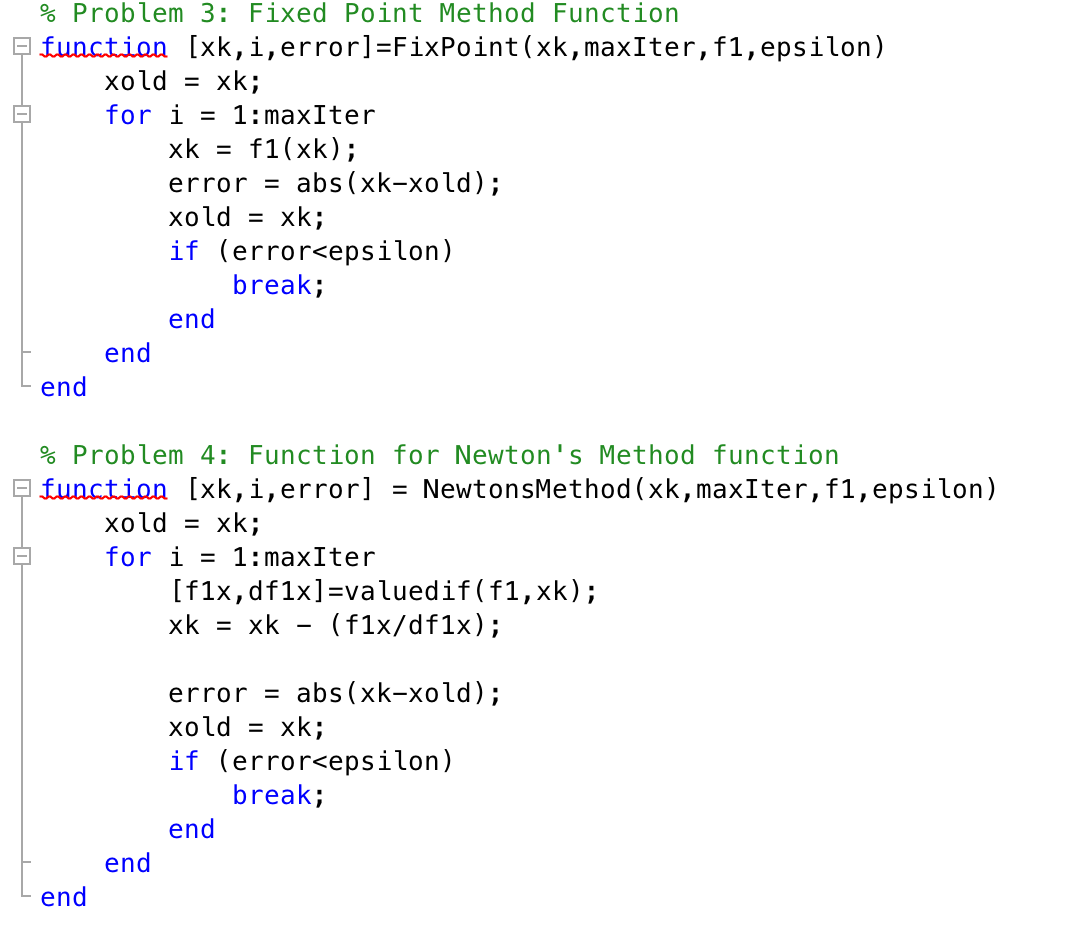
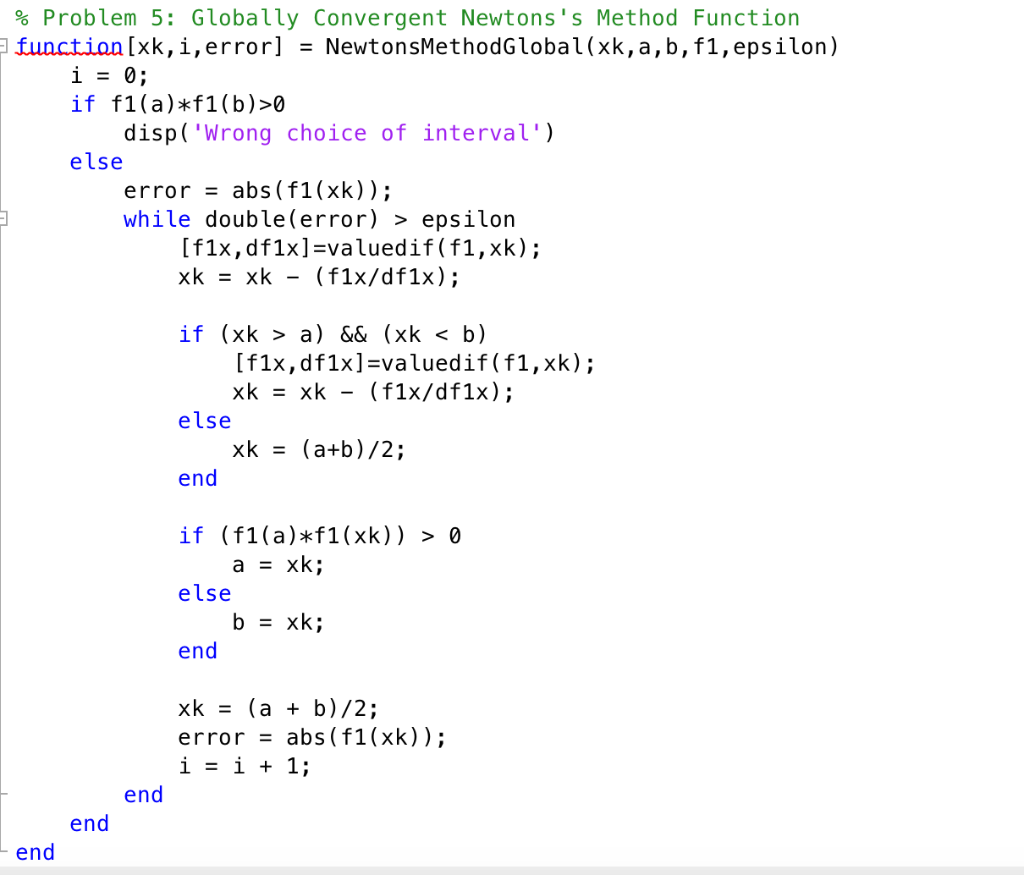
Can someone please do ALL question #6 by editing this part of the code I put below and above, and answering the question "which algorithm is both robust and fast"? I am not sure how to answer #6. I can't get good graphs and not sure why. If possible can you edit the code I put above to get what #6. The code I want edited is this part:

clear; clc; a = -8; b = 8; maxIter = 1e6; %max iteration of the function epsilon = 10e-12; %tolerance value

f1 = @(x) exp(2*sin(x))-x; %function gx = @(x) asin(log(sqrt(x))); %alternative g(x) for problem 3 x0 = 2; %initial guess

% Problem 2: Calling the Interval Bisection Method Function [xk2,i2,error2] = Intbisections(f1,a,b,epsilon);

% Problem 3: Calling the Fixed Point Method Function [xk3,i3,error3] = FixPoint(x0,maxIter,gx,epsilon);

% Problem 4: Calling the Newton's Method function Problem 4 [xk4,i4,error4] = NewtonsMethod(x0,maxIter,f1,epsilon);

% Problem 5: Calling Globally Convergent Newtons's Method Function [xk5,i5,error5] = NewtonsMethodGlobal(x0,a,b,f1,epsilon);

%saving errors as vectors errorVector = [error2,error3,error4,error5];

%Graphing the error vector x_axis = [1,2,3,4]; %x-axis values semilogy(x_axis,errorVector,'-mo'); %graph of error vector in logarithmic y-axis grid on %logarithmic grid (y-axis only)

% Problem 1: Function for calling the value and the derivative of the function function [xvalue, difx] = valuedif(f,x) xvalue = f(xv); syms x if nargout > 1 g(x) = diff(f(x)); difx = double(g(xv)); end end % Problem 2: Interval Bisection Method Function function [xk,i,error] = Intbisections(f, a, b, epsilon) i = 1; if f(a)*f(b)>0 disp('Wrong choice of interval'). else xk = (a + b)/2; error = abs(f(xk)); while error > epsilon if f(a)*f(xk)>0 a = xk; else b = xk; end xk = (a + b)/2; error = abs(f(xk)); i = i + 1; end end end % Problem 3: Fixed Point Method Function function [xk,i,error]=FixPoint(xk, maxIter, f1,epsilon) xold = xk; for i = 1:maxIter xk = f1(xk); error = abs(xk-xold); xold = xk; if (error epsilon) break; end end end % Problem 4: Function for Newton's Method function function [xk,i,error] = NewtonsMethod (xk, maxIter, f1, epsilon) xold = xk; for i = 1:maxIter [f1x,df1x]=valuedif(f1,xk); xk = xk - (f1x/df1x); error = abs(xk-xold); xold = xk; if (error0 disp('Wrong choice of interval'). else error = abs(f1(xk)); while double(error) > epsilon [f1x,df1x]=valuedif(f1,xk); xk = xk - (f1x/df1x); if (xk > a) && (xk 0 a = xk; else b = xk; end xk = (a + b)/2; error = abs(f1(xk)); i = i + 1; end end end clear; clc; a = -8; b = 8; maxIter = 1e6; epsilon = 10e-12; %max iteration of the function %tolerance value f1 = @(x) exp(2*sin(x))-X; gx = @(x) asin(log(sqrt(x))); X0 = 2; %function %alternative g(x) for problem 3 %initial guess % Problem 2: Calling the Interval Bisection Method Function [xk2, i2, error2] = Intbisections (f1, a, b, epsilon); % Problem 3: Calling the Fixed Point Method Function [xk3, i3, error3] = FixPoint(x0, maxIter, gx, epsilon); % Problem 4: Calling the Newton's Method function Problem 4 [xk4, i4, error4] = NewtonsMethod(x0,maxIter, f1, epsilon); % Problem 5: Calling Globally Convergent Newtons's Method Function [xk5, i5, error5] = NewtonsMethodGlobal(x0, a, b, f1, epsilon); %saving errors as vectors errorVector = [error2,error3, error4, error5]; %Graphing the error vector x_axis = [1,2,3,4]; semilogy (x_axis,errorVector,'-mo'); grid on semilogy (kaamis, errorvector, "-mo'); %x-axis values %graph of error vector in logarithmic y-axis %logarithmic grid (y-axis only) raphs of aereor vector in 6. Adjust the above functions such that for each of the four methods, you save the errors lek! for all the iterates into a vector. Draw the four error vectors for the four algorithms, respectively, in the same graph. Generate such graphs corresponding to different initial guesses used in the Newton's method, e.g., X0 = -6, -4, -2,0, 2, 4, 6, as done in Question 3, respectively. From those graphs, what can you say about the performances of the three algorithms? Which algorithm is both robust and fast? % Problem 1: Function for calling the value and the derivative of the function function [xvalue, difx] = valuedif(f,x) xvalue = f(xv); syms x if nargout > 1 g(x) = diff(f(x)); difx = double(g(xv)); end end % Problem 2: Interval Bisection Method Function function [xk,i,error] = Intbisections(f, a, b, epsilon) i = 1; if f(a)*f(b)>0 disp('Wrong choice of interval'). else xk = (a + b)/2; error = abs(f(xk)); while error > epsilon if f(a)*f(xk)>0 a = xk; else b = xk; end xk = (a + b)/2; error = abs(f(xk)); i = i + 1; end end end % Problem 3: Fixed Point Method Function function [xk,i,error]=FixPoint(xk, maxIter, f1,epsilon) xold = xk; for i = 1:maxIter xk = f1(xk); error = abs(xk-xold); xold = xk; if (error epsilon) break; end end end % Problem 4: Function for Newton's Method function function [xk,i,error] = NewtonsMethod (xk, maxIter, f1, epsilon) xold = xk; for i = 1:maxIter [f1x,df1x]=valuedif(f1,xk); xk = xk - (f1x/df1x); error = abs(xk-xold); xold = xk; if (error0 disp('Wrong choice of interval'). else error = abs(f1(xk)); while double(error) > epsilon [f1x,df1x]=valuedif(f1,xk); xk = xk - (f1x/df1x); if (xk > a) && (xk 0 a = xk; else b = xk; end xk = (a + b)/2; error = abs(f1(xk)); i = i + 1; end end end clear; clc; a = -8; b = 8; maxIter = 1e6; epsilon = 10e-12; %max iteration of the function %tolerance value f1 = @(x) exp(2*sin(x))-X; gx = @(x) asin(log(sqrt(x))); X0 = 2; %function %alternative g(x) for problem 3 %initial guess % Problem 2: Calling the Interval Bisection Method Function [xk2, i2, error2] = Intbisections (f1, a, b, epsilon); % Problem 3: Calling the Fixed Point Method Function [xk3, i3, error3] = FixPoint(x0, maxIter, gx, epsilon); % Problem 4: Calling the Newton's Method function Problem 4 [xk4, i4, error4] = NewtonsMethod(x0,maxIter, f1, epsilon); % Problem 5: Calling Globally Convergent Newtons's Method Function [xk5, i5, error5] = NewtonsMethodGlobal(x0, a, b, f1, epsilon); %saving errors as vectors errorVector = [error2,error3, error4, error5]; %Graphing the error vector x_axis = [1,2,3,4]; semilogy (x_axis,errorVector,'-mo'); grid on semilogy (kaamis, errorvector, "-mo'); %x-axis values %graph of error vector in logarithmic y-axis %logarithmic grid (y-axis only) raphs of aereor vector in 6. Adjust the above functions such that for each of the four methods, you save the errors lek! for all the iterates into a vector. Draw the four error vectors for the four algorithms, respectively, in the same graph. Generate such graphs corresponding to different initial guesses used in the Newton's method, e.g., X0 = -6, -4, -2,0, 2, 4, 6, as done in Question 3, respectively. From those graphs, what can you say about the performances of the three algorithms? Which algorithm is both robust and fast