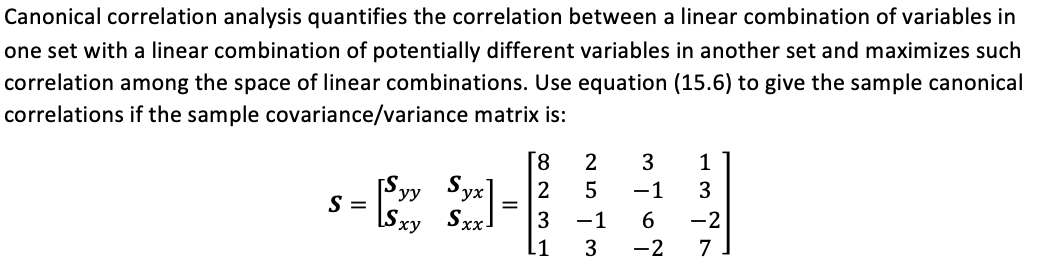
Canonical correlation analysis quantifies the correlation between a linear combination of variables in one set with a linear combination of potentially different variables in another set and maximizes such correlation among the space of linear combinations. Use equation (15.6) to give the sample canonical correlations if the sample covariance/variance matrix is: 8 2 3 1 s E\" Syx]_ 2 5 1 3 ' xy Sxx ' 3 1 6 2 1 3 2 7 S a}, = 535,53an = Hrf. (15.6) i=1 wheres = min(p,q),andr. rip . -,rf aretheeigenvalues ofs;,'s ES\". Notethattheasso- ciation measure R; will be a poor measure, since each of the I. values is between 0 and l, and hence the product of such numbers approach 0 faster. However, the eigenvalues provide a useful measure of association between the vectors. Particularly. the square root of the eigen- values leads to useful interpretations of the measures of the association. The collection of the square root of the eigenvalues {'v r2, .r,} has been named the canonical correlations in the multivariate literature. Without loss of generality we assume that If 2 1% Z 2 r3