can't get this code to work please help

clear all close all syms t r=120*10^-3; c=250*10^-3; w=(500/60); x(t)=r*cos(w.*t)+(c^2-r^2*(sin(w.t)).^2).^(1/2); dx(t)=-r*w^2*cos(w.*t)-(r^2*w*sin(2*w.*t))./(2*((c^2-r^2*(sin(w.*t)).^2).^(3/2))); dxx(t)=-r*w^2*cos(w*t)-((4*r^2*w^2*cos(2*w.*t)*(c^2-r^2*(sin(w*t))^2))+(r^2*w*sin(2*w.*t)).^2)./(4*((c^2-r^2*(sin(w.*t)).^2).^(3/2))); tt=linespace(0,.77,1000); xx1=x(tt); xx2=dx(tt); xx3=dxx(tt); subplot(3,1,1) plot(tt,xx1) grid on xlabel('times(s)') ylabel('position(m)') title('position vs. time') subplot(3,1,2) plot(tt,xx2) grid on xlabel('time(s)') ylabel('acceleration(m/sec^2)') title('acceleration vs time')

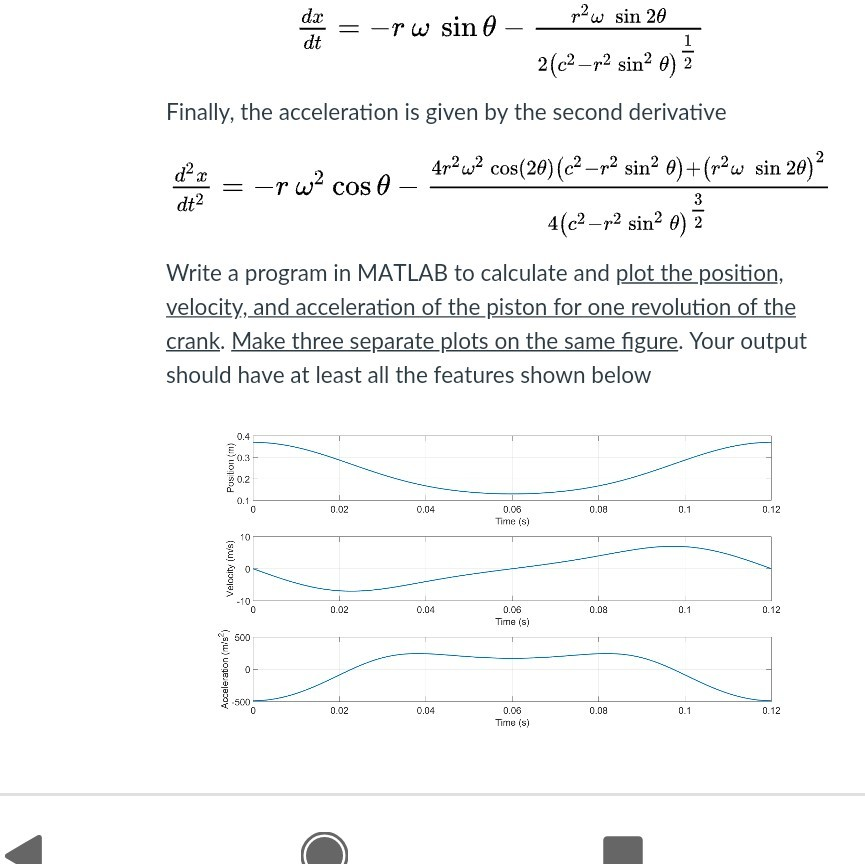
MATLAB Problem 1(50 pts) The piston-crank mechanism is used in many engineering applications. In the mechanism shown below, the crank is rotating at a constant speed of 500 rpmm ces tions l Grades We can assume 0 whent0. Since the angular velocity is constant, we have --wt and the angular acceleration is The geometry of the problem is given by the figure below Which, using the pythagorean theorem, gives So the position of the piston is defined as And the velocity of the piston is the derivative of its position r2 sin 2 dt Finally, the acceleration is given by the second derivative 4,24,2 cos(20) (d-r2 sin2 ) + (r2w sin 29) 2 Write a program in MATLAB to calculate and plot the position. crank. Make three separate plots on the same fgure. Your output should have at least all the features shown below