CBC Cipher question

Please show all work so I can understand fully! :)

With the ECB mode, if there is an error in a block of the transmitted ciphertext, only the corresponding plaintext block is affected. However, in the CBC mode, this error propagates. Lets study the error propagation for CBC mode.

Given we have a cipher that first flips (i.e. convert 1 to 0 and 0 to 1) and then right shifts two bits (circular shift). If we use this cipher in encryption, then the decryption process would be left shift two bits and do a flip. We use this cipher with CBC mode. Assume we have a plaintext as following: 10101100 01110001 11000101, block size is 8. So the plaintext can be divided into three blocks. IV is 01000111. The basic CBC diagram is shown as following

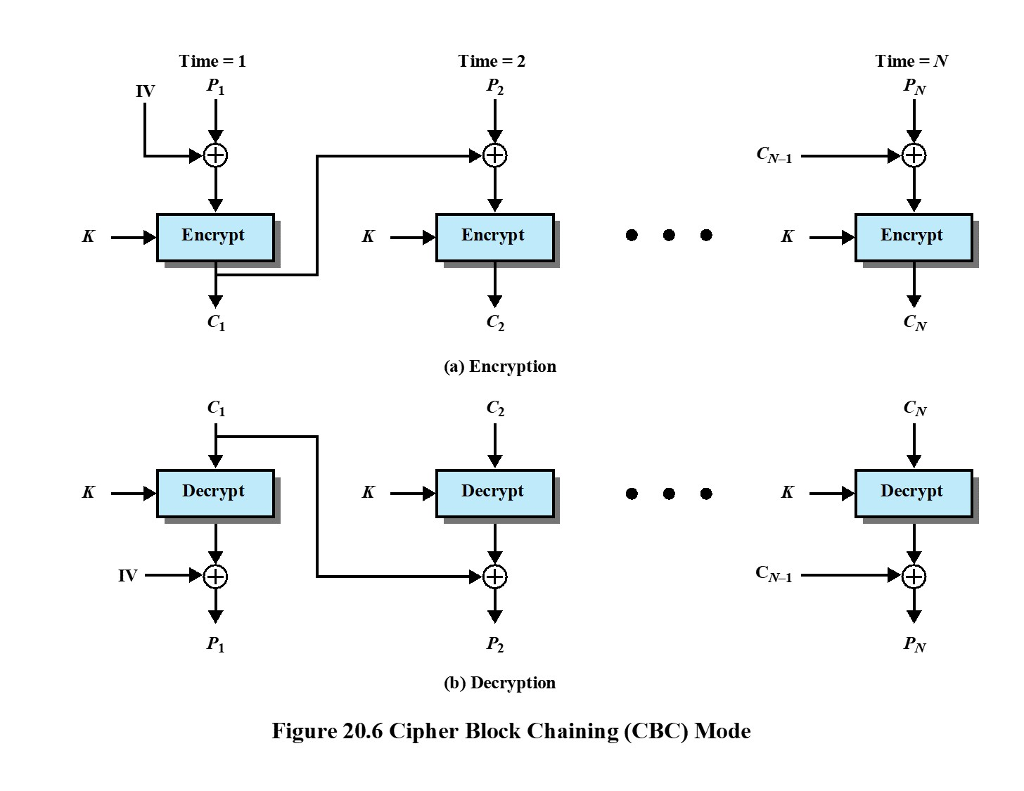
Find ciphertext based on part (a) of the diagram.

Generate the recovered plaintext based on part (b) of the diagram. Show your steps. The recovered plaintext should be same as the original plaintext

Assuming No. 7 bit in the plaintext got bit error (i.e. flipped by accident), the plaintext becomes: 10101110 01110001 11000101. For this plaintext, find the ciphertext and the recovered plaintext again.

Compare the results of the ciphertext and the recovered plaintext from b and c. How does one-bit difference in the first plaintext block affect the ciphertext result and recovered plaintext result?

Time 1 Time 2 Time = N K Encrypt K Encrypt K Encrypt C2 (a) Encryption C2 CN C1 CN K- Decrypt KDecrypt KDecrypt (b) Decryption Figure 20.6 Cipher Block Chaining (CBC) Mode