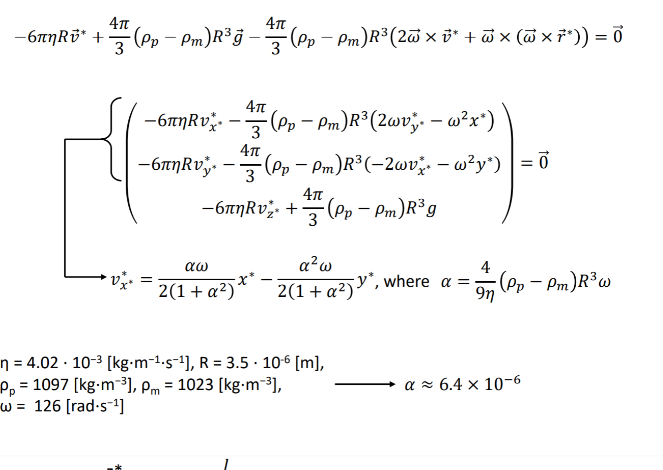
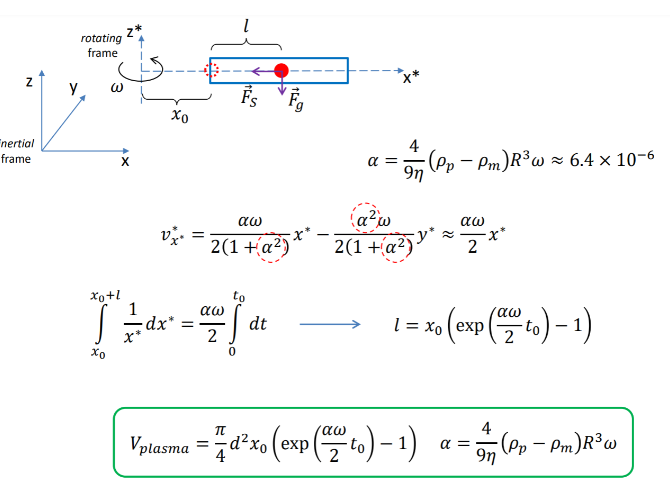
centrifugation", derive the analytical expression for vy, starting from the law of motion in the rotating frame of reference: -banRU+3 (Pp - Pm)Rag -3 (Pp - Pm) R3(20 x d' + a x (@XF))=0 (You must produce a step-by-step derivation of the analytical expression to receive full credit.) [5 points] Where in the tube the velocity, v, is highest? [5 points] What would happen if density of the cell was lower than that of the suspending medium?-6TRU* + 3 ( Pp - Pm) Rag - 2 (Pp - Pm) R3 (20 x v* + Wx (WXF* ) ) =0 -6TRUX 3 ( Pp - Pm) R3 (2wv;. - w2x* ) 3 ( Pp - Pm) R3 (-2wv; - way* ) = 0 -6THRV2+ 2 (Pp - Pm) R3g a 2 w 4 2(1 + a2)* 2(1 + a2) , where a = (Pp - Pm) R3 w n = 4.02 . 10-3 [kg.m-1.5-1], R = 3.5 . 10-6 [m], po = 1097 [kg.m-3], Pm = 1023 [kg-m-3], a =6.4 x 10-6 W = 126 [rad.s-1]rotating frame 7 V XO nertial frame 4 X a = 9n (Pp - Pm)R3 w = 6.4 x 10-6 aw law aw x* 2(1 +a2) X 2(1 +a2) X 2 Xotl to 1 aw dx = at 2 ( 1 - ( 9 0 ) dxa ) ox - Xo Vplasma = axo ( exp ( " w to ) - 1 ) as 4 9n ( Pp - Pm ) R3 w