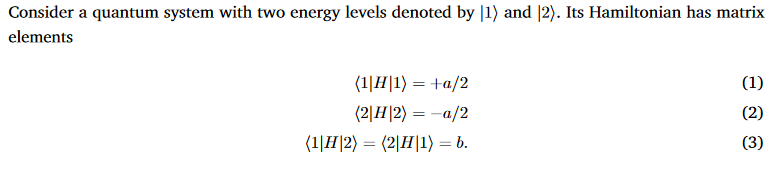
Consider a quantum system with two energy levels denoted by [1) and [2). Its Hamiltonian has matrix elements (1|H|1) = +a/2 (2|H|2) = -a/2 (1|H|2) = (2|H|1) = b. (1) (2) (3) 4. Write H in matrix form. Now, define the transformation matrix U cos(z) sin(z) - sin(z) cos(z) (4) and its transpose UT, and transform H into a rotated"basis by finding the matrix elements of H (2) = UT H U. Show that UT.U = I. 5. Find the value of z for which H(z) becomes diagonal (i.e. set the off-diagonal terms to 0). 6. What are the diagonal matrix elements for this value of z?