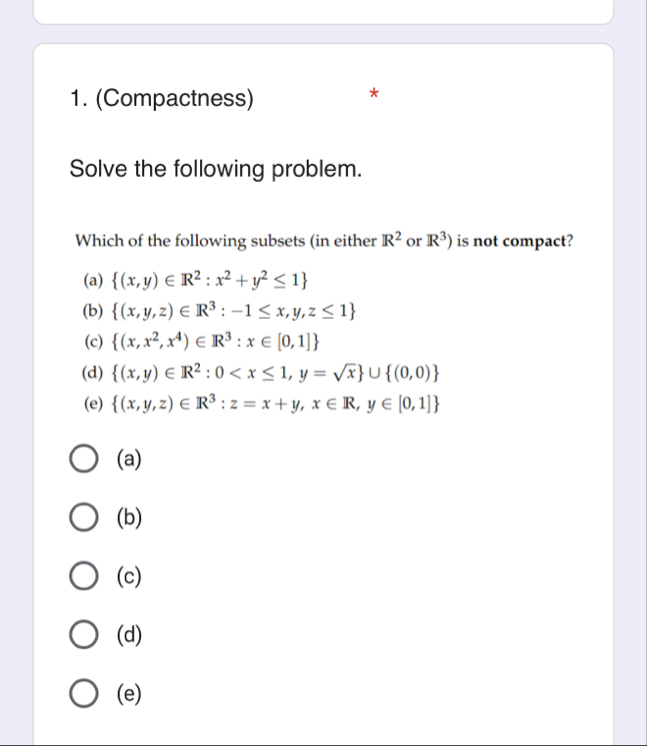
$($Compactness$)$

Solve the following problem.

Which of the following subsets $($in either $R^2$ or $R^3)$ is not compact?

$($a$)\{(x,y)in{R}^2$:$x^2{y}^{2}1\}$

$($b$)\{(x,y,z)in{R}^3$:$-1x,y,z1\}$

$($c$)\{(x,x^2,x^4)in{R}^3$:xin$[0,1]\}$

$($d$)\{(x,y,z)in{R}^3$:$z=xy,$xinR,yin$[0,1]\}$

$($Extreme Value Theorem$)*$

Solve the following problem.

Which of the following statements is true?

$($a$)$ A continuous function defined on a bounded interval that excludes one of its endpoints attains both a maximum and a minimum.

$($b$)$ A function that is differentiable on a closed interval attains a maximum and minimum on that interval.

$($c$)$ The Extreme Value Theorem applies to functions that are continuous on intervals of the form $[a,),$ as long as the function itself is bounded above on that interval.

$($d$)$ A continuous real$-$valued function defined on a compact subset of $R$ attains both its maximum and minimum values.

$($e$)$ The Extreme Value Theorem ensures that the maximum and minimum values of a function occur at interior points of the domain.

$($a$)$

$($b$)$

$($c$)$

$($d$)$

$($e$)$