Question: Process fluid is heated in a series of three stirred tank heaters of the same size. Steam TC Tup(s) where: Steam 2=const G.(s) Controller

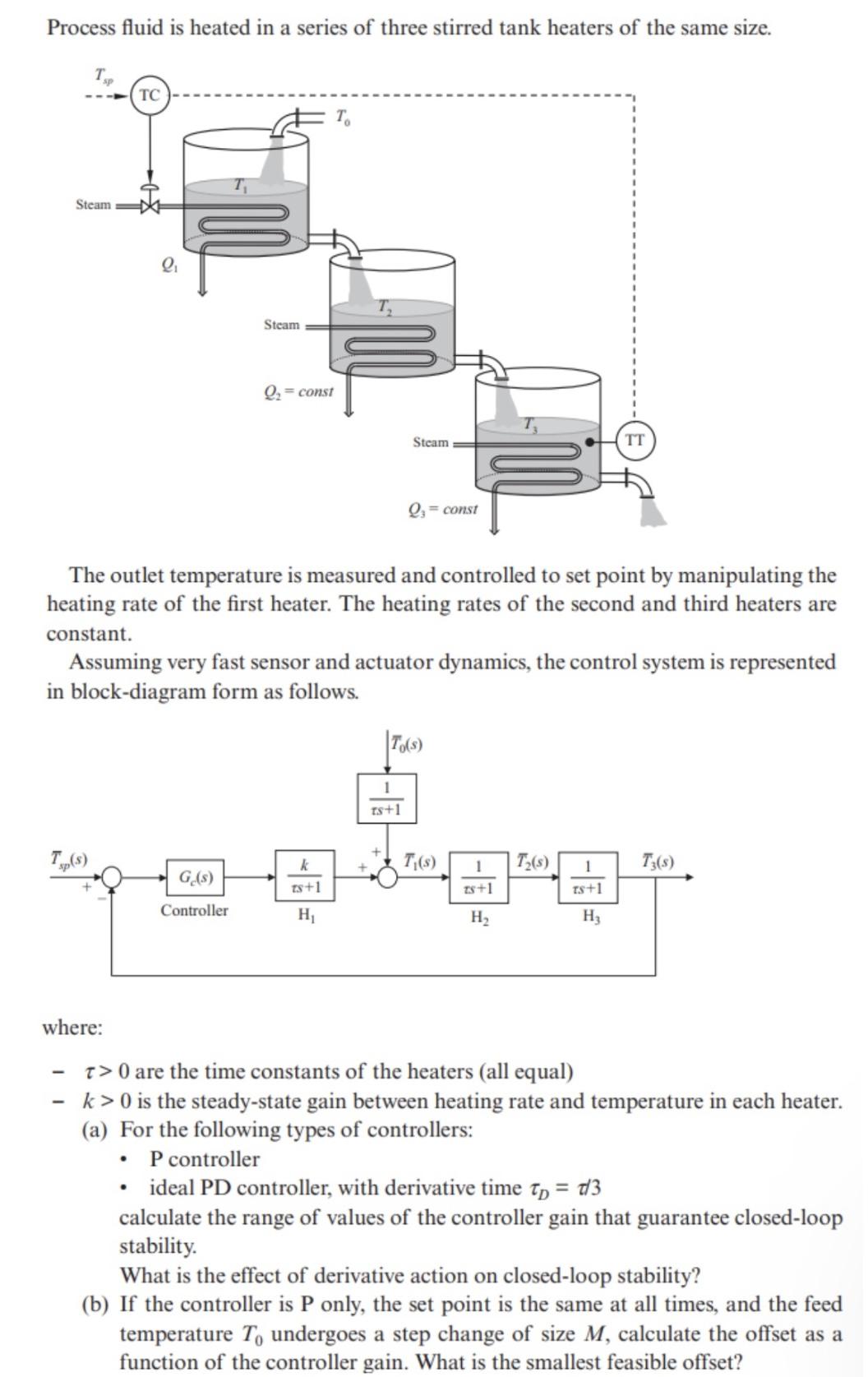
Process fluid is heated in a series of three stirred tank heaters

Process fluid is heated in a series of three stirred tank heaters of the same size. Steam TC Tup(s) where: Steam 2=const G.(s) Controller To The outlet temperature is measured and controlled to set point by manipulating the heating rate of the first heater. The heating rates of the second and third heaters are constant. Assuming very fast sensor and actuator dynamics, the control system is represented in block-diagram form as follows. k ts+1 H Steam Q=const 1 ts+1 To(s) TT T(s) 1 T(s) 1 zs+1 TS+1 H H3 T3(s) T> 0 are the time constants of the heaters (all equal) k>0 is the steady-state gain between heating rate and temperature in each heater. (a) For the following types of controllers: P controller ideal PD controller, with derivative time t = d/3 calculate the range of values of the controller gain that guarantee closed-loop stability. What is the effect of derivative action on closed-loop stability? (b) If the controller is P only, the set point is the same at all times, and the feed temperature To undergoes a step change of size M, calculate the offset as a function of the controller gain. What is the smallest feasible offset?

Step by Step Solution

★★★★★

3.52 Rating (149 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

A new company is planning to make and sell new cheap smart phones in America. They will sell the phone at $99.99 in a market that potentially buys 1 million smart phones every year. They hope to get...

Ann Carter, Chief Financial Officer of Consolidated Electric Company (Con El), must make a recommendation to Con Els board of directors regarding the firms dividend policy. Con El owns two...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

In Problem 10.16, we projected financial statements for Walmart Stores for Years +1 through +5. The data in Chapter 12 Exhibits 12.17-12.19 include the actual amounts for 2012 and the projected...

Consider a home heating system consisting of a natural gas-flied furnace and a thermostat. In this case the process consists of the interior space to be heated. The thermostat contains both the...

The block diagram of a position control system is shown in Figure P12.20. Design a compensator for the particular plant Gp (s) = 1 / s(s2 + 3s + 2) So that the static velocity error coefficient will...

Suppose you have a large supply of books, all the same size, and you stack them at the edge of a table, with each book extending farther beyond the edge of the table than the one beneath it. Show...

A two-input/two-output process involving simultaneous beating and liquid-level changes is illustrated in Figure. Find the transfer function models and expressions for the gains and the Lime constant...

Shown in the figure is a gear-driven squeeze roll that mates with an idler roll, below. The roll is designed to exert a normal force of 30 lbf/in of roll length and a pull of 24 lbf/in on the...

Segmentation is similar to paging but uses variable-sized pages. Define two segment replacement algorithms based on FIFO and LRU page-replacement schemes. Remember that since segments are not the...

You are vacationing in a Wonderland populated by friendly elves and a cannibalistic Cyclops that devours physics students. The elves and the Cyclops look precisely alike (everyone wears loose jeans...

Betty Bodycheck (me = 55 kg. V = 22 km/h in the positive x-direction) and Sally Slasher (ms = 45.0 kg, Vs = 28 km/h in the positive y-direction) are both racing to get to a hockey puck. Immediately...

Prior to adjustment at the end of the year, the balance in Trucks is $300,900 and the balance in Accumulated Depreciation-Trucks is $88,200. Details of the subsidiary ledger are as follows: Truck No....

Express the point given in Cartesian coordinates in spherical coordinates ( , , ) . Note: you really only have to do the work for one, if you use a little geometry and your knowledge of the trig...

Find the area of the region bounded by the graph y 8 %3D 8, and %3D . %3D x2 y 2.

Sketch and find the area of the region enclosed by the semicubical parabola y? = x3 and the line x = 1.

(a) Plot the data on airplane shipments.

19. Evaluate, Vx -1 dx

k=1(2k)!(x+4)k3kFind the interval of convergence. use one of the following tests to determine convergence: Divergent Test, Geometic Series, Intergal Test, P-Series, Ratio Test, Root Test, Comparison...

Consider a shell and tube heat exchanger in which a process fluid is heated by condensing steam generated from a waste heat boiler. The steam valve is used to maintain the outlet process fluid...

12.12 Process fluid is heated in a series of three stirred tank heaters of the same size. The outlet temperature is measured and controlled to set point by manipulating the heating rate of the first...

In the given system, process stream is heated to a specific temperature and after heating it is sent to another process. Process stream is fed to the system at 20C and with 20 m3/h flow rate. Volume...

2. In a system, process stream is heated to a specific temperature and after heating, it is sent to another process. Process stream is fed to the system at 25C and with 15m3/h flow rate. Volume of...