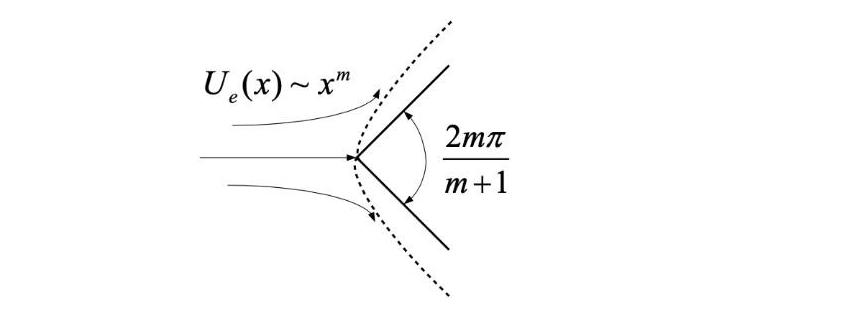
Consider a flow over a wedge (Falkner-Skan problem) whose outer inviscid flow is Ue(x) in terms of a streamfunction Y(x, y) = F(x) f(n) that involves a dimensionless similarity function f(n) of a dimensionless variable n= y g(x). 1. Specify the dimension for F(x) and g(x); Show that the free stream condition demands that F(x) = cU(x)g(x) with some constant c 2. Determine 'all' the possible formats for U. (x) that permits similarity solution. (Expect to obtain Ue(x)~ (x-xo)" or Ue(x) ~ ex, with constant x, m, and a . 3. For the case of Ue(x)~ (x-xo)", determine the compatible g(x). Derive the ODE for f(n) and the corresponding boundary conditions. 4. Deduce the wall shear stress for a general Falkner-Skan flow 5. Determine where the flow will separate; compare the tendency of flow separation in view of wedge angle (happen more quickly on sharper or more blunt wedge) U(x)~ xm 2m m+1