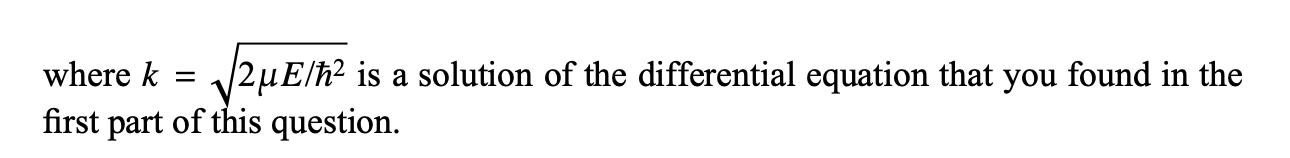
Consider a free particle in three dimensions; its dynamics is determined by the Hamiltonian H = where P2 = P2 + P2 + P2 and u denotes the mass of the particle. We can define two sets of compatible observables: S1 = {H, Px, Py, Pz, ) . S2 = {A, 12, LZ ) . Check that the observables in Si are compatible, and find their simultaneous eigenfunctions. Is the spectrum discrete or continuous? Write the normalisation condition for the eigenfunctions. Consider a generic state described by the wave function (x). Write y(x) as a superposition of the eigenstates of the observables in S1. Show that the coefficients of such a superposition are given by the Fourier transform y (p) of the wave function. What is the probabilistic interpretation of y (p)? Check that the observables in S2 are compatible. Write the set of equations obeyed by their simultaneous eigenfunctions. In particular, find the equation for the radial part of the wave function. Find explicitly the solution for the case & = 0, specifying carefully the boundary conditions. Consider now the case & # 0. Using the ansatz Xe(r) = r+ ne(r), find the differential equation obeyed by ne(r). Check that 1 d sin(kr) ne = Ke r dr krwhere k = 2uE/h2 is a solution of the differential equation that you found in the first part of this