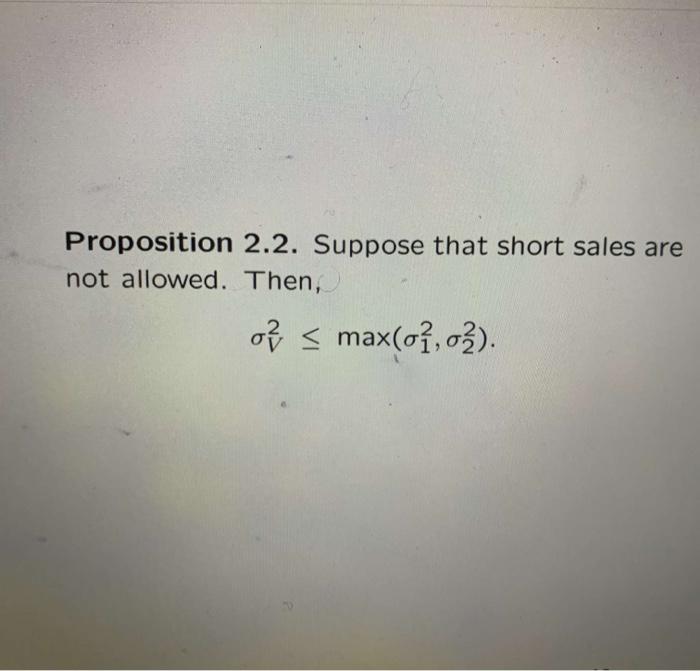
Consider a market model with two securities S, and S2 and three scenarios, 01, 02 and 63 such that P(61) = P(03) = P(@2)/2 = 0.25 Si(0) = 8, S2(0) = 10 S(1) = 6 5 12 for 01 for 02, for 03 S2(1) = { 11 11 9 for 01 for 02 for 03 1. Calculate the quantities o?, oz and P12. 2. Compute the weights in the portfolio with minimum risk for the data above. Does this portfolio involve short selling? 2. Two Securities Proposition 2.1. Consider a portfolio consist- ing of N = 2 securities. Then, the expected return on the portfolio is E[Rv] = E[w1R1+w2R2] = wiE[Ri]+w2E[R2). The variance of the return on the portfolio is VAR[Rv] V AR[w1R1 + w2R2] wV AR[Ru] + w2V AR[R2] +2w1w2COV[R1, R2). Notation 2.1. We denote == 11 E[Ru] 12 E[R2] E[Rv] 0 1 SD[R1] = VVAR[Ru] 02 SD[R2] = VAR[R2] ov SD[Ry] = /VAR[Rv] C12 COV[R1, R2] The correlation coefficient is defined by P12 := C12 0102 Remark 2.1. The correlation coefficient is undefined if 0102 = 0. This condition means that at least one of the assets is risk free. For two risky securities, 01 > 0 and 02 > 0. Thus, P12 is well defined for two risky securi- Proposition 2.2. Suppose that short sales are not allowed. Then, of s max(0,03)