Consider a Markov chain

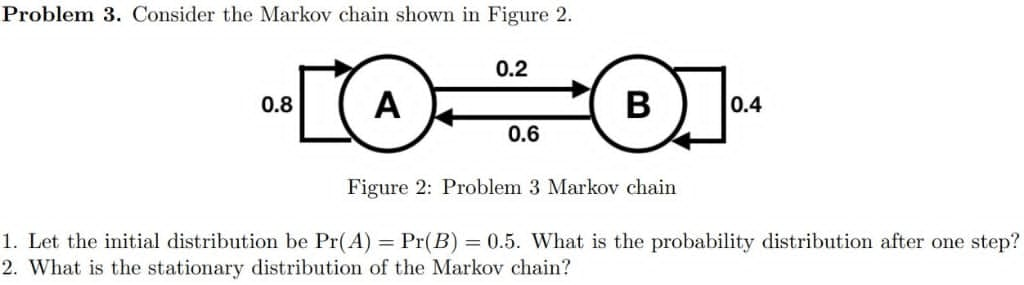
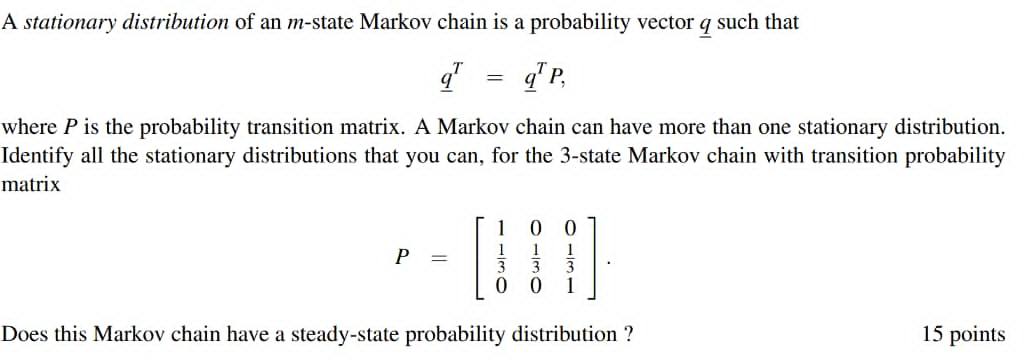
Problem 3. Consider the Markov chain shown in Figure 2. Figure 2: Problem 3 Markov chain 1' Let the initial distribution be Pr(A) = Pr(B) = 0.5. What is the probability distribution after one step? 2. What is the stationary distribution of the Markov chain? A stationary distribution of an m-state Markov chain is a probability vector q such that = q P, where P is the probability transition matrix. A Markov chain can have more than one stationary distribution. Identify all the stationary distributions that you can, for the 3-state Markov chain with transition probability matrix O P Does this Markov chain have a steady-state probability distribution ? 15 pointsFor each of the following transition matrices. determine whether the Markov chain with that transition matrix is regular: (1) is the Markov chain whose transition matrix whose transition matrix Is 0 1 0 0 0.2 0.8 1 0 [J regular? (Yes or No) 5 (2) is the Markovr chain whose transition matrix-whose transition matrix is 0 1 0 [L1 11.4 0.5 0 1 0 regular? (Yes or No) - E (3) Is the Markov chain whose transition matrix whose transition matrix is 1 O 0 0.8 0 0.2 0.8 0.2 0 regular? (Yes or No) (4) is the Markov chain whose transition matrix vmose transition matrix is 0 1 0 08 0 02 O 1 0 regular? (Yes or No) 1. Consider the Markov chain with the following transition matrix. 0 0.5 0.5 0.5 0 0.5 0.5 0.5 0 (a) Draw the transition diagram of the Markov chain. (b) Is the Markov chain ergodic? Give a reason for your answer. (c) Compute the two step transition matrix of the Markov chain. (d) What is the state distribution *, for t = 2 if the initial state distribution for t = 0 is no = (0.1, 0.5, 0.4) T