Question: Consider a single-server queueing system that is initially empty. A customer arrives at time 0, and successive inter-arrival times are exactly x minutes. The

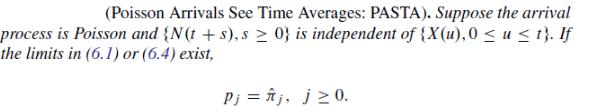
Consider a single-server queueing system that is initially empty. A customer arrives at time 0, and (Poisson Arrivals See Time Averages: PASTA). Suppose the arrival process is Poisson and {N(t+s), s 0} is

Consider a single-server queueing system that is initially empty. A customer arrives at time 0, and successive inter-arrival times are exactly x minutes. The suc- cessive service times are exactly y minutes. Verify Theorem 6.1. Do the limiting probabilities p; exist? Does PASTA (Theorem 6.2) hold? (Hint: Consider the cases y x and y > x separately.) (Poisson Arrivals See Time Averages: PASTA). Suppose the arrival process is Poisson and {N(t+s), s 0} is independent of {X(u), 0 u t}. If the limits in (6.1) or (6.4) exist, Pj = ftj, j0.

Step by Step Solution

★★★★★

3.31 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To verify Theorem 61 and consider the conditions for PASTA Poisson Arrivals See Time Averages lets a... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Operating System Questions!

Report 1: Simmons Food Product Comparison 1. What is the household (HH) index number for ice cream and sherbert ice cream? Is this HH consumption below average, average, or above average? Report 2:...

Let R(A,B,C) be a relation schema, and let R 1 (A,B) and R 2 (A,C) be a decomposition of R. 1) Determine a set F of non-trivial functional dependencies for R such that the decomposition of R in R 1...

Make a list of each of the components necessary for an international contract, identifying which components are extra components that are needed for the contract because of its international status.

Suppose there are 50 companies in a commercial building. Initially there is no automatic fire sprinkler system in the public area of the building. Each company has identical individual demand curve...

In an RC circuit, current flows from the battery until the capacitor is completely charged. Is the total energy supplied by the battery equal to the total energy stored by the capacitor? If not,...

What impressions do you have as you compare these experiences? P-968

6.82 Long Distance It is known that 30% of all calls coming into a telephone exchange are long-distance calls. If 200 calls come into the exchange, what is the probability that at least 50 will be...

Vito York practices medicine under the business title Vito York, M.D. During March, the medical practice completed the following transactions: Mar. 1 York contributed $64,000 cash to the business in...

What are the portfolio weights for a portfolio that has 1 6 0 shares of Stock A that sell for $ 8 9 per share and 1 3 5 shares of Stock B that sell for $ 1 0 2 per share? Note: Do not round...

A slab of polymer 1.6 cm thick, originally at 30C, is heated between steel plates with a surface temperature of 70C. The density of the solid is 950 kg/m 3 , its thermal conductivity is 0.12 W/m K,...

Country: Philippines Topic: Pledge D borrowed P30,000.00 from C. To secure the debt, D pledged his ring, wristwatch, and necklace. Before the debt could be paid, C died leaving X, Y and Z as heirs....

Joe has designed a new smart water filter for industrial applications. Joe calls the water filter the "SMARTY SIEVE". The filter has a novel 3-dimensional shape. Joe asks a Mary to design a logo for...

The interview is not the final stage of the employment process. Background checks are frequently conducted to verify the information provided by applicants on their rsums and application forms and...

QUESTION 4 (a) Study the following balanced scorecard diagram: Financial perspective Customer perspective Learning and Internal growth perspective processes perspective Analyze how balanced scorecard...

1. Production and Inventory Management - Simulation Problem Neo EV is an electrical bus manufacturer headquartered in California. Based on historical sales data and committed contracts, the forecast...

Read the article Why Firms Go Green, Schumpeter, 2011, then: a) What type of single stories do you think internal stakeholders of a company may have in regards to Green initiatives? b) What role do...

on Subhan Enterprises mentaires imprest of Rs. 35,000 Roward these transae t'ion in petty cash book on Subhan Enterprises mentaires imprest of Rs. 35,000 Roward these transae t'ion in petty cash book

1. As a general strategy, would you recommend that Carl take an aggressive approach to capacity expansion or more of a wait-and-see approach? 2. Should Carl go with the option for one facility that...

Read the referenced article that fully describes the management science study summarized in the application vignette presented in Section 2.6. Briefly describe how linear programming was applied in...

Read the referenced article that fully describes the management science study summarized in the application vignette presented in Section 1.3. Summarize the five major reasons given for why...

Reconsider the Special Products Company problem presented in Section 1.2. Although the company is well qualified to do most of the work in producing the iWatch, it currently lacks much expertise in...

=+b. Do the values of the recovered oil appear to be perfectly linearly related to the added oil values? Why or why not?

=+5. The article Objective Measurement of the Stretch-ability of Mozzarella Cheese (J. of Texture Studies, 1992: 185194) reported on an experiment to investigate how the behavior of mozzarella cheese...

=+a. Construct stem-and-leaf displays of both floor area and cost. Comment on any interesting features.