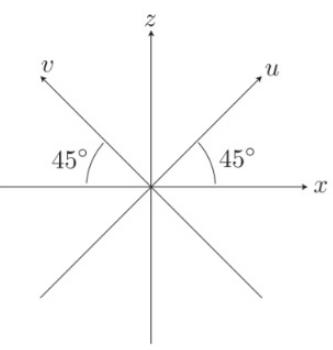
Consider a system of angular momentum 1 = 1. A basis of its state space is formed by the three eigenvectors of L;: +1), 0) and |-1), whose eigenvalues are, respectively, h, 0, and -h. If this system possesses an electric quadrupole moment and is placed in an electric field gradient, its Hamiltonian can be written: H = (L - L) where Lu and L, are the components of L along the two directions in the az plane which form angles of 45 with the r and z axes, as shown in the figure; wo is a real constant. (a) Write the matrix which represents H in the {+ 1), |0), | 1)} basis. What are the eigenstates |E:) of H, and what are their energies? (b) At time t = 0, the system is prepared in the state 1 T(0)) = l + 1) -1- 1)). %3D What is the state vector J(t)) at time t? At t, L; is measured. What are the probabilities of the various possible results? (c) Calculate the mean values (L)(t), (L,)(t) and (L.)(t) at time t. What is the motion performed by the vector (L)(t)? (d) Instead of L;, at time t, a measurement of L? is performed. i. Do times exist when only one result is possible? ii. Assume that this measurement has yielded the result h2. What is the state of the system immediately after the measurement? Indicate, without calculation, its subsequent evolution. 45 45