Question: Consider again the one-period binomial asset pricing model. For a stock, let us write S(0) = S, S(1, ) = S() and S(1, ) =
Consider again the one-period binomial asset pricing model. For a stock, let us write S(0) = S, S(1, ) = S() and S(1, ) = S(). (Assume here that S() > S()). Let F be the t = 1 forward price of the stock. Let C be the (t = 0) value of the ATM call on the stock. Let (as usual) R be the value in CAD at t = 1 of 1 CAD at t = 0. Show the following:
1.S() S2 = S()S() F = S() + (1 )S() C = find , S() and S() in terms of S, R, F, C. Hint: Show that S() = and that the right hand side of (3.32) exceeds F. This leads to an alter- native calibration of the the binomial asset pricing model. Remark 3.23. This is the basis of an idea used by Derman and Kani of Goldman-Sachs (NY) in 1994 [24]. The idea is that S,R,F,C are market information that will allow us to compute the possible values S() and S().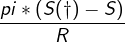
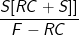 (3.32)
(3.32)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


