Question: Consider an orbital angular momentum l ( l is an integer and positive or zero ) and a spin s = 1 2 . We
Consider an orbital angular momentum l l is an integer and positive or zeroand a spin sWe now define a total angular momentum j and we want to derive the states j l mj with mj l To do this, we consider the angular momentum descent operator Fx iFy for any angular momentum F We call F an angular momentum if it satisfies the commutator relations for angular momentum. Only from these commutator relations can we conclude for the eigenstates of such an angular momentum operator:
F mF hbar F mF
We now want to apply this equation to the angular momenta l and s
Show that starting from j l mj l l ml l; s ms by applying the operator j jx ijy gives picture:
bHow can you analogously construct additional missing vectors of the subspace j l
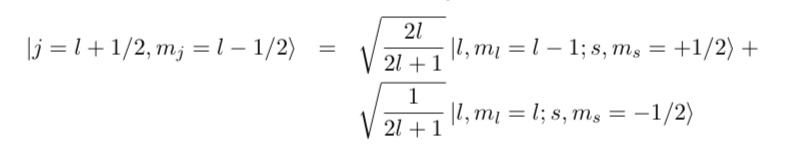
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


