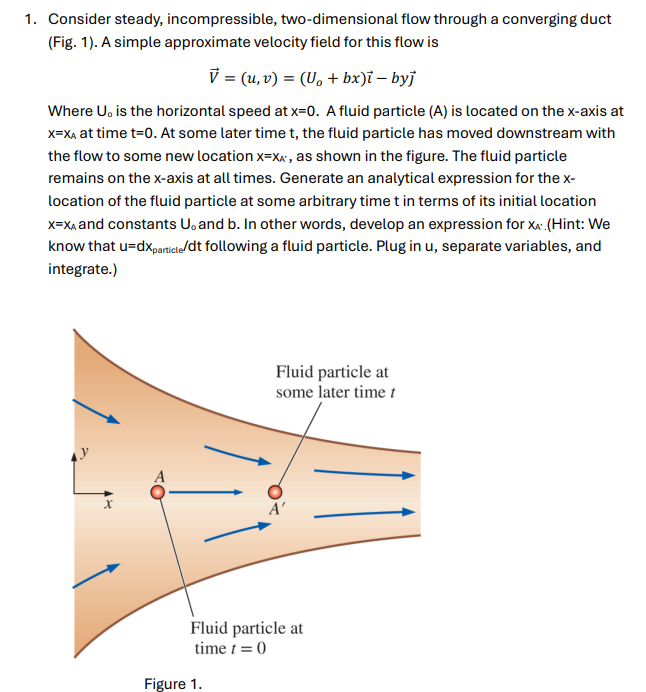
Consider steady, incompressible, two$-$dimensional flow through a converging duct

$($Fig$.1).$ A simple approximate velocity field for this flow is

vec$(V)=(u,v)=(U_o+bx)vec()-$byvec$()$

Where $U_0$ is the horizontal speed at $x=0.$ A fluid particle $(A)$ is located on the $x-$axis at

$x=x_A$ at time $t=0.$ At some later time t $,$ the fluid particle has moved downstream with

the flow to some new location $x=x_{A^{\text{'}}},$ as shown in the figure. The fluid particle

remains on the x$-$axis at all times. Generate an analytical expression for the x$-$

location of the fluid particle at some arbitrary time $t$ in terms of its initial location

$x=x_A$ and constants $U_O$ and b $.$ In other words, develop an expression for $x_{A^{\text{'}}}.($Hint: We

know that $u=d\frac{x_{\text{p}\text{a}\text{r}\text{t}\text{i}\text{c}\text{l}\text{e}}}{d}t$ following a fluid particle. Plug in u $,$ separate variables, and

integrate.$)$

Figure $1.$