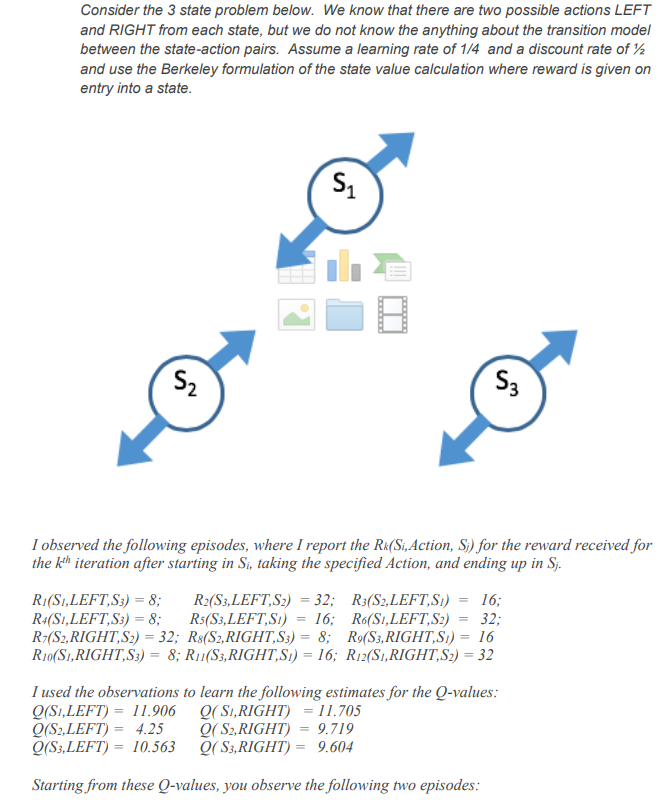
Consider the 3 state problem below. We know that there are two possible actions LEFT and RIGHT from each state, but we do not know the anything about the transition model between the state-action pairs. Assume a learning rate of 1/4 and a discount rate of and use the Berkeley formulation of the state value calculation where reward is given on entry into a state. Si S2 Sz I observed the following episodes, where I report the Rk(Si, Action, S) for the reward received for the kth iteration after starting in Si, taking the specified Action, and ending up in Sj. R(S,LEFT,S3) = 8; R2(S3,LEFT,S2) = 32; R3(S2,LEFT,SI) R4(SI,LEFT,S3) = 8; R5(S3,LEFT,SI) 16; R6(SI,LEFT,S2) 32; R (S2, RIGHT.S2) = 32; R$(S2, RIGHT,S3) = 8; R9(S3, RIGHT,SI) = 16 RIO(S.,RIGHT,S3) = 8; R.(S3, RIGHT,SI) = 16; R:2(S.,RIGHT.S2) = 32 16; I used the observations to learn the following estimates for the Q-values: Q(S,LEFT) = 11.906 (S,RIGHT) = 11.705 Q(S2,LEFT) = 4.25 (S2,RIGHT) = 9.719 Q(S3,LEFT) = 10.563 Q(S3, RIGHT) = 9.604 Starting from these Q-values, you observe the following two episodes: R13(S2, RIGHT,SI) = 16 R14(S),RIGHT,S3) = 8 3 questions (show all your work neatly): a) What are the best estimates for the Q-values after these two additional observations? b) What is appropriate policy for all states if you wish to exploit this learned information? c) What is the estimated transition model based on the above information? (sketch above) Clearly indicate your answers to each questions below, and sketch the transition model above with estimated probabilities shown. Consider the 3 state problem below. We know that there are two possible actions LEFT and RIGHT from each state, but we do not know the anything about the transition model between the state-action pairs. Assume a learning rate of 1/4 and a discount rate of and use the Berkeley formulation of the state value calculation where reward is given on entry into a state. Si S2 Sz I observed the following episodes, where I report the Rk(Si, Action, S) for the reward received for the kth iteration after starting in Si, taking the specified Action, and ending up in Sj. R(S,LEFT,S3) = 8; R2(S3,LEFT,S2) = 32; R3(S2,LEFT,SI) R4(SI,LEFT,S3) = 8; R5(S3,LEFT,SI) 16; R6(SI,LEFT,S2) 32; R (S2, RIGHT.S2) = 32; R$(S2, RIGHT,S3) = 8; R9(S3, RIGHT,SI) = 16 RIO(S.,RIGHT,S3) = 8; R.(S3, RIGHT,SI) = 16; R:2(S.,RIGHT.S2) = 32 16; I used the observations to learn the following estimates for the Q-values: Q(S,LEFT) = 11.906 (S,RIGHT) = 11.705 Q(S2,LEFT) = 4.25 (S2,RIGHT) = 9.719 Q(S3,LEFT) = 10.563 Q(S3, RIGHT) = 9.604 Starting from these Q-values, you observe the following two episodes: R13(S2, RIGHT,SI) = 16 R14(S),RIGHT,S3) = 8 3 questions (show all your work neatly): a) What are the best estimates for the Q-values after these two additional observations? b) What is appropriate policy for all states if you wish to exploit this learned information? c) What is the estimated transition model based on the above information? (sketch above) Clearly indicate your answers to each questions below, and sketch the transition model above with estimated probabilities shown