Question: Consider the Ax = b system 2x1 + 4x2 +63 + 4x4 = b 2x15x2+7x3+ 6x4 = b2. 2x1 +3x2+5x3 + 2x4 = b3

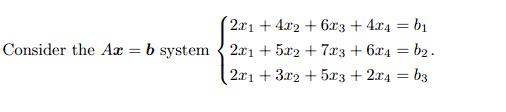
Consider the Ax = b system 2x1 + 4x2 +63 + 4x4 = b 2x15x2+7x3+ 6x4 = b2. 2x1 +3x2+5x3 + 2x4 = b3

Consider the Ax = b system 2x1 + 4x2 +63 + 4x4 = b 2x15x2+7x3+ 6x4 = b2. 2x1 +3x2+5x3 + 2x4 = b3 (a) Reduce [A b] to [U c] so that Ax = b becomes a triangular system Ux = c. (b) Find the conditions on b, b2, b3 for Ax = b to have a solution. (c) Describe the column space of A. Is it a line or is it a plane. Is it in R? (d) Describe the nullspace of A by writing down the special solutions. Is the nullspace in R4? (e) Reduce [U c] to [R d] and determine the special solutions and the particular solution. (f) Find a particular solution to Ax = 3 and then the complete solution. 5

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Q 1 ) When the Manarosa Beach Resort developed a marketing campaign aimed to attract business customers, institutions, and organizations that needed a location to hold 2 - day to 4 - day conferences,...

Edney Company employs a standard cost system for product costing. The per-unit standard cost of its product is: Raw materials Direct labor (2 direct labor hours x $8.00 per hour) Manufacturing...

Use the modified algorithm developed in Exercise 9 to solve the linear systems in Exercise 8. In Exercise 7 a. 2x1 x2 = 3, x1 + 2x2 x3 = 3, x2 + 2x3 = 1. b. 4x1 + x2 + x3 + x4 = 0.65, x1 + 3x2 x3...

In 2010 Casey made a taxable gift of $7.3 million to both Stephanie and Linda (a total of $14.6 million in taxable gifts). Required: Calculate the amount of gift tax due this year and Caseys unused...

As an automobile moves along the road, the vertical displacements at the tires act as the motion excitation to the automobile suspension system [16]. Figure FIGURE AP8.3 Auto suspension system model....

5. How much voice and input would you recommend Andrea give to the staffers as the Blaze transitions to its new normal? What are the pluses of giving such input and what would be the dangers...

6.14 A normal random variable x has an unknown mean and standard deviation or =2. If the probability that X exceeds 7.5 is 0.8023, find .

You now have $3000. You will toss a fair coin four times. Before each toss you can bet any amount of your money (including none) on the outcome of the toss. If heads comes up, you win the amount you...

Will is a proprietor who uses the cash method of accounting. During the current year he receive payments as follows: cash $100 for work he did this year a customer agreed to pay him 200 for services...

How to prepare income statement and a common sized income statement from the following information. Sales $525,000 Cost of goods sold 200,000 General and administrative expenses 62,000 Depreciation...

need question 12 and 13 answered 12. 20 years ago, my dad was riding his bike along a country road and noticed someone dumping garbage on this property. The property was designated to have natural...

80% of the arrivals to a COVID19 vaccination center pre-register themselves on the COWIN portal before arriving whereas the rest walk in and register at the venue. Pre-registered individuals verify...

Vignette Assumption When completing the vignettes, there is a vignette assumption. That is, when reading assume that a full assessment has been done and no mention means 'no evidence'. This is the...

1. The following diagram shows a glancing collision of mass 1 and mass 2. Assume that the masses are the same and the surface has no friction. Before Collision After Collision horizontal Mass 2 axis...

Name 3 things that Pals restaurant did that made them a unique fast food restaurant.

The Elberta Fruit Farm of Ontario is considering buying a cherry - picking machine to replace the part - time workers it usually hires to harvest its annual cherry crop. The machine shakes the cherry...

1. Which of the four major types of information systems do you think is the most valuable to an organization? 2. How do you critically associate the ideas of business agility and business efficiency...

Use the combinatorial definition of the determinant to evaluate (a) (b) 30000 04000 00100 00020 00005 04000 00010 00300 00002 50000

Repeat Exercise 18 under the assumption that the relationship between the current I and the voltage drop V is best modeled by an equation of the form V = IR + c, where c is a constant offset value....

Indicate whether the statement is always true or sometimes false. Justify your answer with a logical argument or a counterexample. (a) If A is a singular n n matrix, then Ax = 0 has infinitely many...

Use the properties of radicals to solve for y in each of the following instances. (a) 3y=6x5 Squaring both sides of the equation, then using Rule 1, (3y) = (6.15)2 3y = 36x10 y = 12x10 (b) 7y=42x...

Using the properties of radicals set forth in Section 1.5, simplify the following radicals. (a) 27 == +9 (Rule 3) (b) 5.45 (c) 245 3 27 3-27 = 81 = 5 45 5.45 = 225 = 15 = 55.4949 = 75 245= (d) 108 ==...

Add or subtract the following fractions by finding the least common denominator. (a) To find the least common denominator, use the fundamental principle of arithmetic to decompose the denominators...