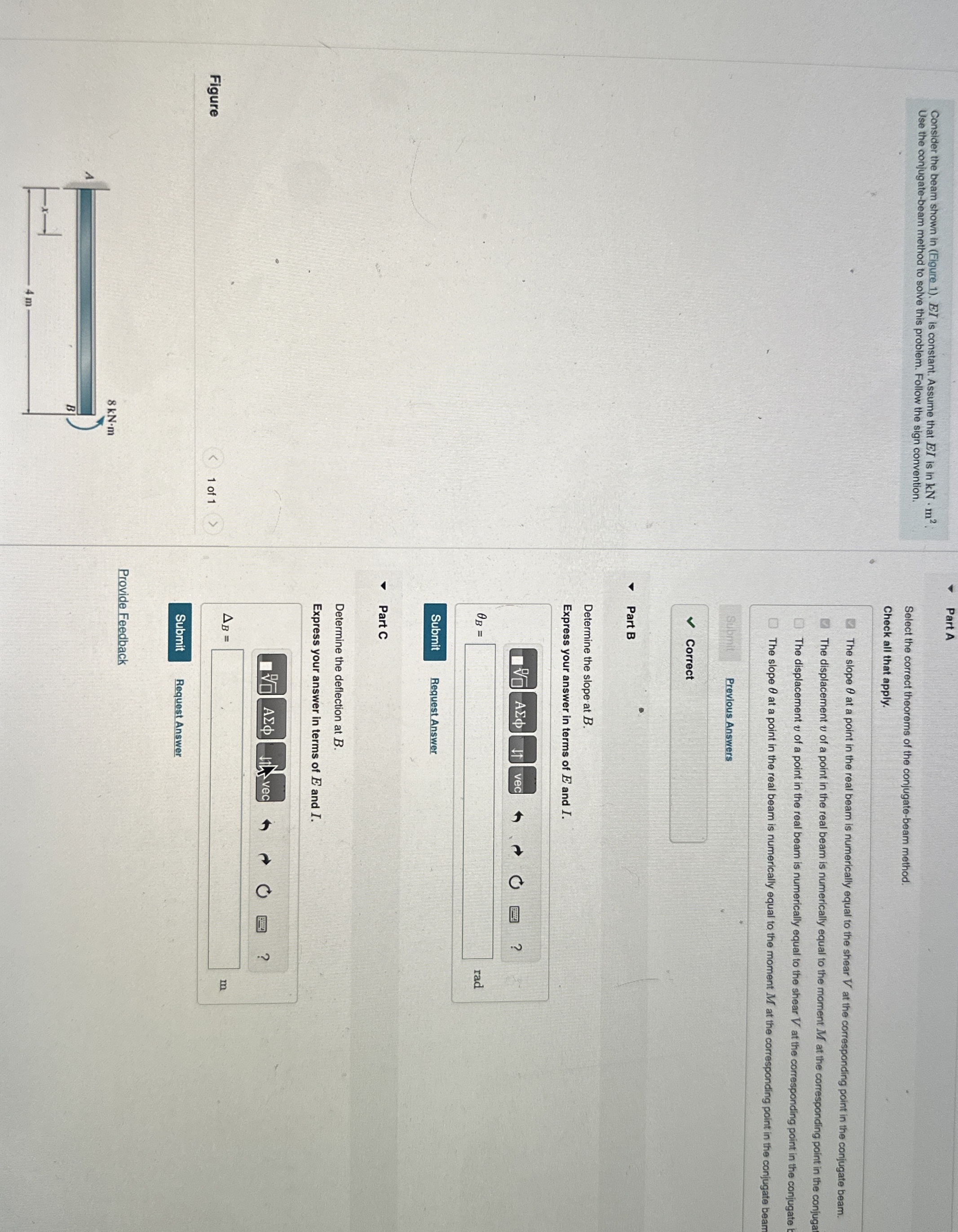
Consider the beam shown in $($Figure $1).$ EI is constant. Assume that $EI$ is in $kN*m^2$ : Use the conjugate$-$beam method to solve this problem. Follow the sign convention.

Part A

Select the correct theorems of the conjugate$-$beam method.

Check all that apply.

The slope $$ at a point in the real beam is numerically equal to the shear $V$ at the corresponding point in the conjugate beam.

The displacement $v$ of a point in the real beam is numerically equal to the moment $M$ at the corresponding point in the conjugat

The displacement $v$ of a point in the real beam is numerically equal to the shear $V$ at the corresponding point in the conjugate $b$

The slope $$ at a point in the real beam is numerically equal to the moment $M$ at the corresponding point in the conjugate beam

Submit

Previous Answers

Correct

Part B

Determine the slope at $B.$

Express your answer in terms of $E$ and I.

Request Answer

Part C

Determine the deflection at $B.$

Express your answer in terms of $E$ and I.

Figure

$1$ of $1$

$?$

$$

AE $$

vec

$?$

${}_B=$

$$

Request Answer

Provide Feedback

ANSWER EVERYTHING PLS