Consider the beam shown in $($Figure $1).$ Suppose that w

$=360$ N$/$m

$.$

Figure$1$ of $1$

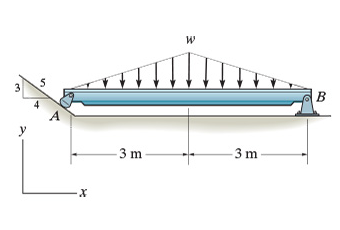
An inclined surface extends upward and leftward so that the surface lies along the hypotenuse of a right triangle with its horizontal leg of $4$ units, a vertical leg of $3$ units, and a hypotenuse of $5$ units. A straight horizontal beam is rocker supported on the inclined surface with its left end $\text{'}$A$\text{'}$ and pin supported on a horizontal surface with its right end B$.$ A distributed load acts vertically downward on the beam. The load first increases linearly from $0$ at point $\text{'}$A$\text{'}$ to w at the midpoint of the beam $3$ meters away from the ends. Then it decreases linearly back to $0$ at point B$.$ The x y plane is shown. The x axis is directed to the right, and the y axis is directed upward.

Part A

Determine the magnitude of reaction at A

$.$

Express your answer to three significant figures and include the appropriate units

Activate to select the appropriates template from the following choices. Operate up and down arrow for selection and press enter to choose the input value typeActivate to select the appropriates symbol from the following choices. Operate up and down arrow for selection and press enter to choose the input value type

FA

$=$

nothing

nothing

Request Answer

Part B

Determine the x

and y

components of reaction at B

using scalar notation.

Express your answers in newtons to three significant figures separated by a comma.

Activate to select the appropriates symbol from the following choices. Operate up and down arrow for selection and press enter to choose the input value type

Bx

$,$ By

$=$

nothing

N