Consider the data $(x_i=(x_1^{(i)},x_2^{(i)}),y^{(i)}{)}_i=1^n$ below, where we fit the model $p(y=1|x,w)=(w_0+w_1{x}_1+w_2{x}_2).$

Suppose we fit the model by the Lasso regularized negative $log-$likelihood objective function, i$.$e$.,$ we minimize

$J\{w,b\}=\frac{1}{n}{\displaystyle \underset{1}{\overset{n}{}}}log(1+$exp$(-y^{(i)}(tilde(x{)}^{(i)T}w)))+{\displaystyle \underset{j=1}{\overset{d}{}}}|w_j|$

where tilde$(x{)}^{(i)}=(1,x^{(i)}).$

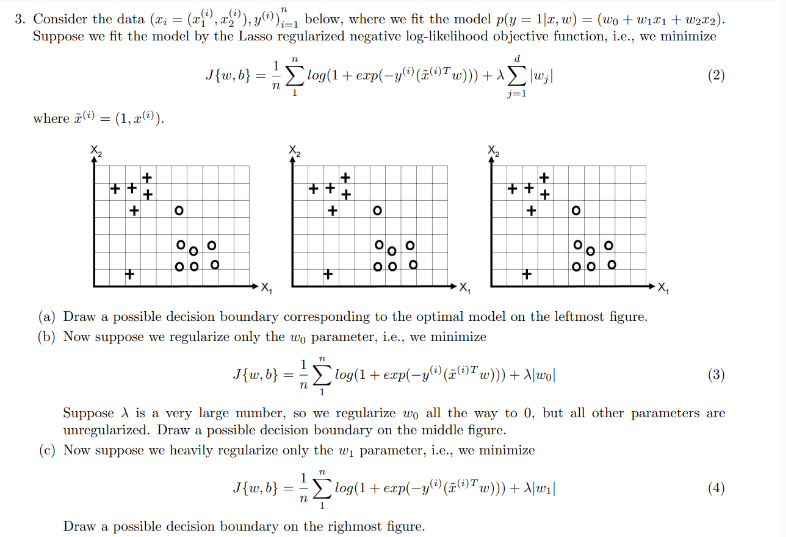
$($a$)$ Draw a possible decision boundary corresponding to the optimal model on the leftmost figure.

$($b$)$ Now suppose we regularize only the $w_0$ parameter, i$.$e$.,$ we minimize

$J\{w,b\}=\frac{1}{n}{\displaystyle \underset{1}{\overset{n}{}}}log(1+$exp$(-y^{(i)}(tilde(x{)}^{(i)T}w)))+|w_0|$

Suppose $$ is a very large number, so we regularize $w_0$ all the way to $0,$ but all other parameters are

unregularized. Draw a possible decision boundary on the middle figure.

$($c$)$ Now suppose we heavily regularize only the $w_1$ parameter, i$.$e$.,$ we minimize

$J\{w,b\}=\frac{1}{n}{\displaystyle \underset{1}{\overset{n}{}}}log(1+$exp$(-y^{(i)}(tilde(x{)}^{(i)T}w)))+|w_1|$

Draw a possible decision boundary on the righmost figure.